ここは半球状をした撮影スタジオの中です。 壁はすべて真っ黒で背景が映らないようになっています。 Ａ君は未来型の360度平面撮影動画カメラを持って撮影しています。 ＢさんはＡ君の北側 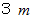離れたところにいて南を向いたままで足踏みをしています。

　 Ａ君はカメラの狙いの中心をＢさんに向けたまま、 Ｂさんの周囲を反時計回りにＢさんとの距離を保ったまま１周しました。 今Ａ君の撮った動画を再生しますと、 Ｂさんは原点（ カメラの位置であり映像の中心です ） の上側 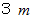の位置にいて、 時計回りに１自転したように映っています。 これを 映像 とします。

　 今度は、 カメラを北の方向に向けたまま、 Ｂさんの周囲を反時計回りにＢさんとの距離を保ったまま１周しました。 今Ａ君の撮った動画を再生しますと、 Ｂさんは原点を中心とする半径 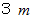の円軌道上を南向きのまま反時計回りに１周したように映っています。 これを 映像 とします。

　 今度は、 カメラの狙いの中心をＢさんに向けたままＡ君は移動せずに、 Ｂさんが南を向いたままＡ君の周囲を反時計回りにＡ君との距離を保ったまま１周しました。 今Ａ君の撮った動画を再生しますと、 Ｂさんは原点の上側 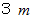の位置にいて、 時計回りに１自転したように映っています。 これを 映像 とします。

　 今度は、 カメラを北の方向に向けたままＡ君は移動せずに、 Ｂさんが南を向いたままＡ君の周囲を反時計回りにＡ君との距離を保ったまま１周しました。 今Ａ君の撮った動画を再生しますと、 Ｂさんは原点を中心とする半径 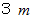の円軌道上を南向きのまま反時計回りに１周しています。 これを 映像 とします。

　 映像 と 映像 、 および、 映像 と 映像 は同じ映像になっています。 映像 を「 移動回転座標法 」と言い、 映像 を「 移動無転座標法 」と言い、 映像 を「 不動回転座標法 」と言い、 映像 を「 不動無転座標法 」と言うことにします。 そして、 映像 と 映像 と 映像 を「 主観的撮影法 」と言い、 映像 を「 客観的撮影法 」と言うことにします。

　移動と回転をあわせて「 時空間運動 」と言うことにし、 映像 と 映像 、および、 映像 と 映像 が同じ映像になっていることを、「 時空間運動の相対原理 」と言うことにします。

　ここで問題です。「 時空間運動の相対原理 」は、 物質が２つのとき、 つまり、 観察する側の物質と観察される側の物質が１つずつのときにのみ成立し、 観察される物質が２つ以上あるときは破綻するのではないかということです。 この問題を解くために、 Ｂさんと同じ位置にいて南を向いたまま足踏みをするＣ君に登場してもらいます。 ただし、 Ｃ君は途中で１回以上Ｂさんとは違う動きをしなくてはなりません。

　Ａ君はカメラの狙いの中心をＢさんに向けたまま、 Ｂさんの周囲を反時計回りにＢさんとの距離を保ったまま１周しました。 このときＣ君はＡ君と全く同じ速度で南を向いたまま移動しました。 今Ａ君の撮った動画を再生しますと、 Ｂさんは原点の上側 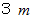の位置にいて、 時計回りに１自転したように映っています。 そして、 Ｃ君は原点を向いたまま時計回りに１周しているように映っています。 これを 映像 とします。

　 今度は、 カメラを北の方向に向けたまま、 Ｂさんの周囲を反時計回りにＢさんとの距離を保ったまま１周しました。 このときＣ君はＡ君と全く同じ速度で南を向いたまま移動しました。 今Ａ君の撮った動画を再生しますと、 Ｂさんは原点を中心とする半径 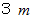の円軌道上を南向きのまま反時計回りに１周したように映っています。 そして、 Ｃ君は最初とおなじ位置で南を向いたまま足踏みを続けているように映っていました。 これを 映像 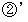とします。

　 今度は、 カメラの狙いの中心をＢさんに向けたままＡ君は移動せずに、 Ｂさんが南を向いたままＡ君の周囲を反時計回りにＡ君との距離を保ったまま１周しました。 このときＣ君は最初とおなじ位置で足踏みを続けました。 つまり、 Ｃ君はＡ君と全く同じ速度の大きさ で南を向いたまま移動しました。 今Ａ君の撮った動画を再生しますと、 Ｂさんは原点の上側 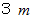の位置にいて、 時計回りに１自転したように映っています。 そして、 Ｃ君は原点を向いたまま時計回りに１周しているように映っています。 これを映像 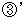とします。

　 今度は、 カメラを北の方向に向けたままＡ君は移動せずに、 Ｂさんが南を向いたままＡ君の周囲を反時計回りにＡ君との距離を保ったまま１周しました。 このときＣ君は最初とおなじ位置で足踏みを続けました。 つまり、 Ｃ君はＡ君と全く同じ速度の大きさ で南を向いたまま移動しました。 今Ａ君の撮った動画を再生しますと、 Ｂさんは原点を中心とする半径 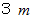の円軌道上を南向きのまま反時計回りに１周しています。 そして、 Ｃ君は最初とおなじ位置で南を向いたまま足踏みを続けています。 これを 映像 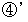とします。

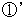　 映像 と 映像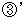 、 および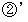、 映像 と 映像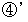 は同じ映像になっています。 ということは、 観察される物質が多数のときも「 時空間運動の相対原理 」は成立していそうです。

　 さて、「 座標とはカメラアングルである。」と言えます。 もっと言えば、「 座標とは、 運転席から見た目盛り付きフロントガラスの中の風景である。」と言えます。 さらに言うと、「 座標とは観察者である。」と言えます。 座標は動きません。 その理由は、 観察者が観察者自身に対して相対的に静止しているからです。 観察者が加速度運動をする場合には、 観察者が観察する物質の時空間運動は「 みかけの力 」によることになります。 この「 みかけの力 」を導入しますと、「 時空間運動の相対原理 」が完成します。 ２つの物質が異なる方向に等速直線運動をしているときに、 どちらが移動していてどちらが静止しているのかを決めることはできません。 なぜならば、 ２つの物質には全く力が作用していないからです。 ２つの物質の相対的加速度運動のときに「 みかけの力 」を導入しておくと、 見方を変えるとどちらの物質にも力が働いていることになりますので、 どちらが静止してどちらが運動しているのか区別できないのです。

　「 座標とは観察者である。」という観点から、 特殊相対性理論のローレンツ変換後の斜交座標とは何か考えてみましょう。 もちろん、 ローレンツ変換前の直交座標は普通の観察者です。 私は、 普通の観察者のことを「 ニュートン力学的観察者 」と言っています。 定説の特殊相対性理論では、 ローレンツ変換後の斜交座標は観察されている人になっています。 ですから、 移動している人が持っている時計の針は、 静止している人が持っている時計の針よりもゆっくりと回転しており、 移動している人が持っている物差しの目盛の幅は、 静止している人が持っている物差しの目盛の幅よりも短くなっているのです。 私は、 ローレンツ変換後の斜交座標はローレンツ変換前の観察者と同人物であると考えています。 それも、 ローレンツ変換後の斜交座標は、 観察される物の立場に立った観察者であり、 観察される物が観察者となる直交座標系を元の観察者が観察した座標であると考えています。 私は、 観察される物の立場に立った観察者のことを「 相対論的観察者 」と言っています。 そして私は、「 ニュートン力学的観察者 」の立場に立った観察者の観察内容 と「 相対論的観察者 」の立場に立った観察者の観察内容を比較してあれこれ言っても無意味であると、 定説に対して批判しています。