電場、 磁束密度、 磁場 は次の式で表されます。

　　　電場 ：
　　　　　　　

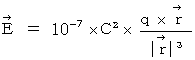
　　　磁束密度 ：
　　　　　　　
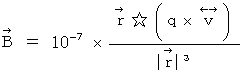
　　　　　　　　コメント ：
　　　　　　　　　　 　
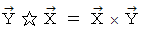
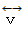　　　　　　　　　　 　 は、 と 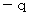の電荷が重なっていて電気的に
　 　　　　　　　　　　　ゼロの状態から、 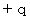と 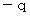の電荷が分かれていくときの 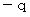の電
　 　　　　　　　　　　　荷に対する 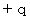の電荷の相対的速度を表します。

　　　磁場 ：
　　　　　　　


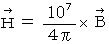
　 私は、 電場を光の速さで割ったものを 「 実質電場 」 と言っています。 また私は、 電束密度のことを 「 実質磁場 」 と言っています。 それらは次のように表されます。

　実質電場 ：
　　　　　　

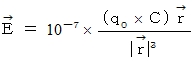
　　　　　　　　　すると、 クーロン力 は次の式で表されます。
　　　　　　　　　　　　　　

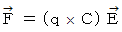
　実質磁場 ：
　　　　　　

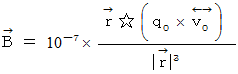
　　　　　　　　　すると、 ローレンツ力 は次の式で表されます。
　　　　　　　　　　　　　　

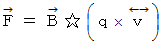
すると、 マックスウェルの電磁方程式 は次のような美しい形になります。
　　　　　　
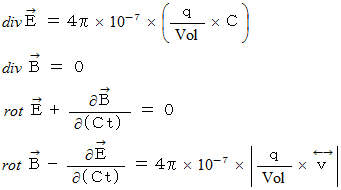
　　　　　　　　　　　※　ここではＥは電場ではなく、電場をＣで割った実質電場を表しています。

　 私がこのようにしている理由は、 特殊相対性理論にあります。「 電場を作るのは単なる電荷ではなく、 固有時間を光の速さ で移動している電荷である。」と考えることによって、 磁場を作るローレンツ力 と 電場を作るクーロン力 との統一が見えてくるからです。 固有時間を虚数とすれば、 電場と磁場の相対論的統一が可能なのです。 アインシュタインの特殊相対性理論とは、 ４次元時空間においては物質の運動は電磁波の運動と同じ形態を取るものと仮定し、 物質の移動に関する直交座標系と斜交座標系との座標変換を、 時間を虚数とすることにより直交座標系と直交座標系との等長座標変換に置き換えて簡明化し、 それから導かれる矛盾する現象を現実のものであるとする理論です。

コメント ：
　直交座標系と斜交座標系との座標変換であれば、 たとえば、「 君よりも私に近い所に存在する物質は、 君よりも私から見た目のほうが大きい。」ということが納得できるのですが、 直交座標系と直交座標系との等長座標変換に置き換えてしまうと、「 私から見れば、 君が見た目よりも小さくはなく、 君から見れば、 私が見た目よりも小さくはないか。 いったいその物質はどこにあんねん？　あっ、そや、 手前にあるものを君は老眼鏡で見とんのや。」というコメントになってしまいます。