ある商品を生産するために機械Aと機械Bが使われます。 その生産効率は、機械Aは 8個/分、 機械Bは 2個/分 です。 機械Aでは5%の確率でエラー商品ができ、 機械Bでは10%の確率でエラー商品ができます。 商品を無作為に1個抽出したときエラー商品でした。 これが機械Bで作られた確率はいかほどでしょうか?
条件付き確率は 「 時系的後ろ向き確率 」 です。 一方、 一般的な確率は 「 時系的前向き確率 」 で、 将来起こることの予想になります。 一般的な確率問題では、 上記の文章に続いて 「 商品を無作為に1個抽出したとき、 エラー商品である確率を求めよ。」 ということになり、 答えは 0.8 × 0.05 + 0.2 × 0.1 =→ 0.06 =→ 6% となりますが、 条件付き確率問題では 「 商品を無作為に1個抽出したときエラー商品であった。 これが機械Bで作られた確率を求めよ。」 となります。 そしてその解法の1手段として、次の「 正方形確率分布図 」を作成するという方法があります。
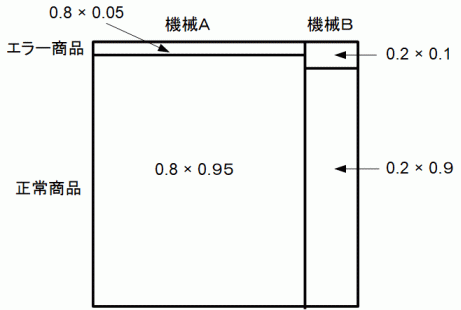
答えは ( 0.2 × 0.1 ) ÷ ( 0.8 × 0.05 + 0.2 × 0.1 ) =→ 1 / 3 です。
もう一つの解法の手段は。ベン図を作る方法です。
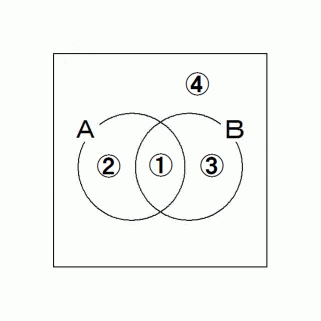
確率分布: ① + ② + ③ + ④ = 1
A: 先発命題( 真偽不明;確率的予想可 )
B: 後発命題 = 真であるという事実 = 入手情報
A
調査物質が集合Bに含まれているという情報を得た時点で、
それが集合Aにも含まれている確率が、条件付き確率 である。
条件付き確率 = ① ÷ ( ① + ③ )
集合B: 抽出された商品であり、かつ、エラー商品
① { 2÷(8+2) } × 0.1 =→ 0.02
③ { 8÷(8+2) } × 0.05 =→ 0.04
① ÷( ① + ③ ) = 0.02 ÷ 0.06 =→ 1/3
 確率 へ戻る
確率 へ戻る