問題 1 :

 がそれぞれ4個ずつ計32個あります。
がそれぞれ4個ずつ計32個あります。この中から4個を選ぶ方法は何通りあるでしょうか?
また、 この中から4個を選んで1列に並べる方法は何通りあるでしょうか?
-
4個を選ぶ方法は重複組み合わせですから、 次のようにして答えを求めることができます。
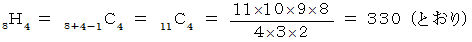
( 理 由 )
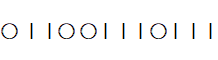
⇒ ① 1個 + ③ 2個 + ⑥ 1個
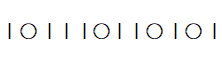
⇒ ② 1個 + ⑤ 1個 + ⑦ 1個 + ⑧ 1個
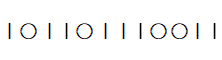
⇒ ② 1個 + ④ 1個 + ⑦ 2個
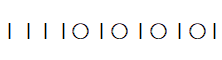
⇒ ⑤ 1個 + ⑥ 1個 + ⑦ 1個 + ⑧ 1個
4個の 〇 と 8個の 楔棒 の順列であると捉える。
左から2番目の楔棒は ② を表し、① を表す楔棒 と ② を表す楔棒 との間にある 〇 の数が ② の 個数を表す。
順列の最後( 右端 )は必ず楔棒になる。
したがって、右端の楔棒は無視する。すると、4つの例はそれぞれ次のようになる。
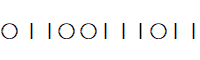

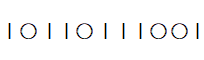
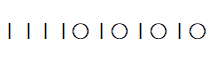
したがって、4+7個 の スペースのうち 〇 が占める4個のスペースの組み合わせの数だけ並べ方がある。
A : 同じ数が含まれない場合
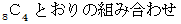
B : 3種類の数が含まれている場合
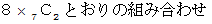
C : 2種類の数が2個ずつの場合
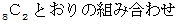
D : 1種類の数が3個有る場合
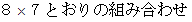
E : 同じ数ばかりの場合 8とおりの組み合わせ
A : 例えば、
 、
、  、
、  、
、  の並べ方
の並べ方 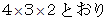
B : 例えば、
 、
、  、
、  、
、  の並べ方
の並べ方 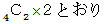
C : 例えば、
 、
、  、
、  、
、  の並べ方
の並べ方 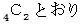
D : 例えば、
 、
、  、
、  、
、  の並べ方 4とおりの組み合わせ
の並べ方 4とおりの組み合わせE : 例えば、
 、
、  、
、  、
、  の並べ方 1とおりの組み合わせ
の並べ方 1とおりの組み合わせしたがって、 答えは、
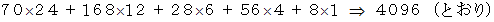
 確率 へ戻る
確率 へ戻る