（１） 重複組み合わせ

　 赤、青、黄、緑、白、黒 のボールが６個ずつあります。 これら36個のボールから５個を選ぶとき、色の組み合わせ方は何通りあるでしょうか？

　　　　　

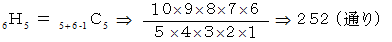
十進BASIC のプログラムで確かめてみましょう。

（２） 疑似重複組み合わせ

　 赤、青、黄、緑、白、黒 のボールが３個ずつあります。 これら18個のボールから５個を選ぶとき、 色の組み合わせ方は何通りあるでしょうか？

　 もし、それぞれのボールが５個以上あるとしましょう。その場合は、重複組み合わせになります。
　　　　一色だけの場合の数は ６ 通り です。
　　　　一色が４個ある場合の数は ６ × ５ ＝ 30 通り です。
　　　　したがって、 答えは 252 − ６ − 30 ＝ 216 通り です。

十進BASIC のプログラムで確かめてみましょう。

（３） 重複組み合わせの公式を導く

　 赤色セーターを着た人、 青色セーターを着た人、 黄色セーターを着た人、 緑色セーターを着た人、 白色セーターを着た人、 黒色セーターを着た人 の６人がいて、 ボールが５個あります。 この５個のボールすべてを彼らに分配する場合の数を考えましょう。 ０個しかもらえない人も含めて考えます。

　 が５個あるとき、黒色セーターの人以外が、 から の仕切り棒を順番に１つずつ置いていき、 それよりも左側の をすべて獲得していきます。 黒色セーターの人は白色セーターの人が置いた仕切り棒よりも右側の をすべて獲得します。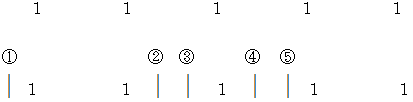

　　　　　

上のように仕切り棒が置かれたとき、 ボールの配分は次のようになります。
　　　　　赤色セーターを着た人 ：　０個　　　　　　　青色セーターを着た人 ：　２個
　　　　　黄色セーターを着た人 ：　０個　　　　　　　緑色セーターを着た人 ：　１個
　　　　　白色セーターを着た人 ：　０個　　　　　　　黒色セーターを着た人 ：　２個

　 このような 仕切り棒 と の配列関係の場合の数は、 一列に並べられた ５ ＋ ６ − １ 個の椅子から が座れる５つの椅子の組み合わせを考えるのと同じことです。 したがって、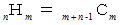 となります。