【 問 題 1 】
-
椅子が7個一列に並べられています。 男性4人、女性3人がいます。 男性の名前は、 あい君、 かい君、 さい君、 たい君 で、 女性の名前は、 はいさん、 まいさん、 やいさん です。
彼らは、 あいうえお順に好きな席に着いていきます。
(1) ただし、 女性3人が連なるように配慮しながらです。 何通りありますか?
(2) ただし、 女性が隣同士にならないように配慮しながらです。 何通りありますか?
-
最初に、 7個の椅子をどかしてください。
(1) まず、 女性3人をさしあたり1人の人とみなして、 5人の順列を考えます。
その場合の数は、 5! =→ 5 × 4 × 3 × 2 × 1 =→ 120 とおり
女性3人が一列に並ぶ場合の数は、 3! =→ 6 とおり
したがって、 答えは 6 × 120 =→ 720 とおりです。
(2) まず、 男性4人が一列に並ぶ場合の数を考えます。 4! =→ 24 とおりです。
次に、 男性の列の中に前後を含めて椅子を 1 個ずつ入れていきます。 椅子は5個必要です。
そして、 この5個の椅子が3人の女性を迎え入れる場合の数を考えます。
5P3 =→ 5 × 4 × 3 =→ 60 とおり
または、 この5個の椅子から3個を選んで、どの順で女性が着くかを考えます。
5C3 × ( 3 × 2 × 1 ) =→ 5 × 4 × 3 =→ 60 とおり
したがって、 答えは 60 × 24 =→ 1440 とおりです。
-
色以外には区別のないおはじきがあります。 赤が4個、 青が3個、 黄が2個です。 これら9個のおはじきを一列に並べる場合の数を求めなさい。
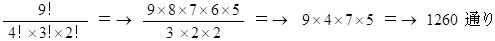
 確率 へ戻る
確率 へ戻る