ｍ 人 が １ 列に並べられた ｎ 個 の椅子に座る、 すべての場合の数は、 _ｍＰ_ｎ 通り です。 今回は、 順列 ： _ｍＰ_ｎ の由来について考えます。 そして、 順列 ： _ｍＰ_ｎ よりも、 組み合わせ ： _ｍＣ_ｎ のほうが先に出来たということを申し上げたいと思います。

　 _ｍＰ_ｎ の原型は、 _ｍＰ_ｍ です。 つまり、 ｍ 人 が １ 列に並べられた ｍ 個 の椅子に座る、 すべての場合の数です。 それは ｍ！ 通り です。 順列 ： _ｍＰ_ｎ は ｍ！ が原点となっています。

　 ｍ！ の次に誕生したのは、 ｍ 人 の中から ｎ 人 を選択する、 すべての場合の数です。 それは、 組み合わせ ： _ｍＣ_ｎ 通り です。 ｍ 人 を ｎ 人 と （ ｍ − ｎ ）人 の２つのグループに分け、 それぞれのグループでの順列の原型を考えます。 すると、 それらは次のようになります。
　　　　_ｍＣ_ｎ 通り
　　　　ｎ！ 通り
　　　　（ ｍ − ｎ ）！ 通り
そして、 これら３つを掛け合わせたものが、 ｍ！ 通り になっているという次の式が誕生します。
　　　　_ｍＣ_ｎ × ｎ！ × （ ｍ − ｎ ）！ 　＝　ｍ！
したがって、 次の定義が誕生します。
　　　　

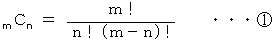
最後に、 順列 ： _ｍＰ_ｎ の定義が誕生します。 それは、 次の式です。
　　　　
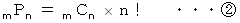
したがって、
　　　　

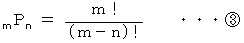
一般的には、 次の式が頻回に使われています。
　　　　
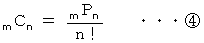
しかし、 元々は、 の式であり、 の式なのです。