（１） 光粒子説 と 光波動説

　 私が一般相対性理論の出だしからつまづいてしまう理由は、 光粒子説を ４９％、 光波動説を ５１％ 支持していてる 光波動説派 であるためではないかと思います。

光の速さを 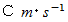とします。
　 点 から 離れた所に、 点光源 があります。 この光源から一瞬放たれて四方八方に広がっていく光の一部は、 秒後に 点 に到着します。 この現象をどう捉えるかです。
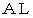　 アインシュタインは、 光粒子説を唱えていましたので、 一瞬のうちに四方八方に放たれた無数の光子の中の１つが、 点 に届いているように考えたのではないかと思います。 これに対して私は、 一個の光子（ 波動説では光子と言わないが ） が、 空洞の球面状になって拡大していき、 その中の１点が、 点 に衝突するイメージを持ってしまいます。 したがって、「 点 にとっての 結果的光軌跡 は 線分 である。」となります。

　 この現象を、 線分 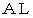の垂直二等分線上を一定の加速度で加速的変速直線運動をしている観察者の立場から見てみましょう。
　 光粒子説であれば、 アインシュタインが一般相対性理論の中で言っているとおりのことだろうと思います。 つまり、 観察者からすると、 光子 や 点光源 や 点 には、 見かけの力が働き、 光子も垂直方向には、 一定の加速度で変位します。 そこで私たちは、 特殊相対性理論で言われている光の速さは普遍であるという概念は、 観察者が加速度運動をしていないことや重力が働いていなことが前提であることに気づきます。 そこで、 アインシュタインは、 放物線的な光子の軌跡が最短距離であるから、 観察者にとっての曲線分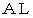 は「 内側から見た 歪んだ空間の中における 直線 」であると結論し、 光速普遍不変の原理を貫きます。

　 これに対して、 光波動説は次のように説明すると思います。 観察者にとって光は最短コースを通るから、 光子は垂直方向には変位せず、 したがって、「 結果的光子軌跡 」は、 直線分 になる。 空間は歪んでなんかいない。

（２） エレベータの中と外との逆転の発想

　 そういうことならば、 光粒子説派になって一般相対性理論を理解してみようではありませんか。 つまり、 相対性理論においては、 光のイメージを、 四方八方に広がる光ではなくて、 レーザー光とするのです。

　「 自由落下している広大な正方形の床を持つガラス張りのエレベータの中にいる観察者からすると、 エレベータの向かい合う壁の同じ高さに取り付けられた 発光点 から 受光点 に向けて、 伝わる光の運動の軌跡は直線であるが、 地上にいる観察者にとっては、 伝わる光の運動の軌跡は、 発光点 を頂点とし受光点 を通る放物線である。」というのが、 有名な一般相対性理論の最初の命題です。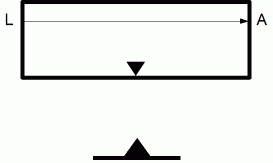

　　　　　　　

　 実は、 エレベータの中の観察者は無重力空間にいる人の象徴で、 地上にいる観察者は加速度運動をしているロケットの中にいる人の象徴なのです。 ですから、 アインシュタインが考えた自由落下しているエレベータの思考実験は、 次のように書き換えた方が理解しやすいのです。
　「 無重力空間において、 静止している発光点 から放たれた光が静止している受光点 に届く。 それを、 線分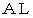 の垂直二等分線上で静止している人が観察するのと、 線分 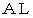の二等分線上を等加速度運動するロケットの中にいる人が観察するのとでは違いがある。（ そのロケットは、 広大な正方形の床を持つガラス張りのロケットで、 床から天井に向けての方向に飛行するものとする。 また、 光が放たれた瞬間のロケットの初速を とする。） 前者の光の運動の軌跡は直線であるが、 後者の光の運動の軌跡は、 発光点 を頂点とし受光点 を通る放物線である。」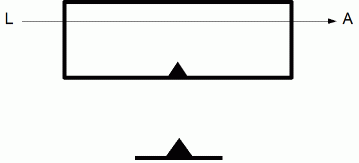

　　　　

　 エレベータの思考実験のほうが現実的で取り着きやすいのですが、 なぜ、 エレベータの思考実験のほうが難しいのでしょうか。 それは、「 等価原理 」が入っているからです。 一般相対性理論の理解の駆け出しの人に、 最初から等価原理はキツイのです。 等価原理の真髄は、「 質量が近似的に作る一様な重力場と、 等加速度運動している空間が作る相対的一様重力場とは、 区別することができない。」というものです。