上図の物質Ａの質量は m₁ kg で、物質Ｂの質量は m₂ kg です。しばらくすると衝突し、その後物質Ａは右向きに速さ v'₁ m/s で物質Ｂは右向きに速さ v'₂ m/s で等速直線運動しました。２つの物質の反発係数は e です。
　運動量保存の法則より、次の式が成り立ちます。
　　　　m₁v₁ ＝ m₁v'₁＋m₂v'₂　　　・・・ �@
　反発係数の式より、次の式が成り立ちます。
　　　　
　　　　
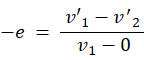
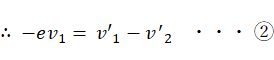
�@ と �A の連立方程式を解くと、次のようになって、衝突後の物質Ａと物質Ｂの速度が分かります。
　　　　

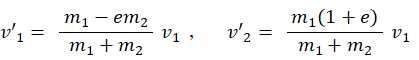
　さて、衝突後の物質Ａと物質Ｂの速度をもっと簡単に知ることができます。それは、２物質系の重心速度を用いる方法です。

　２物質系の重心は次の式で表されます。（ 物質Ａの位置ベクトルを 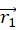物質Ｂの位置ベクトルを 　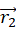とします。）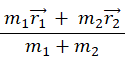
　　　　
　　　　　　　　※ 参照： 大学生のための物理学 ＞ 剛体力学 ＞ 物質系の重心ベクトル
　これを t で微分すれば次の重心速度 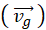になります。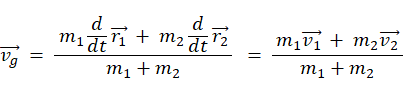
　　　　

　保存力以外の外力が加わらない限り運動量の総和は一定であるという「運動量保存の法則」がありますが、例えば等速直線運動をしている２つの物質の衝突のように、運動量保存の法則が成り立っているとき、重心速度は一定です。ですから、重心と並走している観察者の系で衝突の前後の２つの物質の運動状態を比較することができます。ちなみに、物質Ａや物質Ｂと常に並走している観察者の系で衝突の前後の２つの物質の運動状態を比較することはできません。なぜなら、衝突によって瞬間的に観察者の速度が変わるので、慣性系を乗り換えることになるからです。

　重心と並走している観察者の座標系では、衝突前の物質Ａの速度は次のようになります。
　　　　
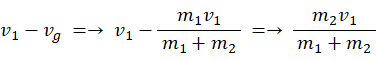
　重心と並走している観察者の座標系では、衝突前の物質Ｂの速度は次のようになります。
　　　　
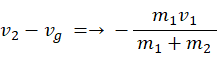
　重心と並走している観察者の座標系では、衝突後の物質Ａの速度は次のようになります。
　　　　
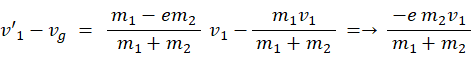
　重心と並走している観察者の座標系では、衝突後の物質Ｂの速度は次のようになります。
　　　　
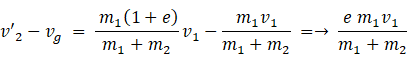
　これらから、次の２つの式が成り立っていることが分かります。
　　　　
　　　　
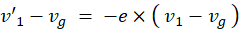
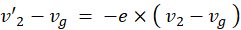
　というわけで、重心と並走している観察者の座標系では、衝突前の物質の速度に−e をかけさえしてやれば、衝突後の物質の速度が簡単に分かるということが解りました。

　作用反作用の関係にある力は、多数の物質系として見たときに、内力と言われます。内力だけしか働かない物質系では、物質系の重心は、静止を含む等速直線運動をします。したがって、物質系の重心に並走している観察者の座標系は、絶対静止系であると言うことができます。物質系の重心が静止している場合は、紙面の読者の座標系が絶対静止系になります。絶対静止系における物質の移動速度を「 重心相対速度 」と言うことにします。２つの物質の反発係数を e とすると、衝突後の重心相対速度は、衝突時の重心相対速度に −e をかけたものになります。