(1) マクロ的に見る
-
点A上に質量 m1 の物質が存在し、点B上に質量 m2 の物質が存在する。 点A と 点B との距離は L である。
以上のシチュエーションをマクロ的に見ると、 線分AB上の点Aからの距離が
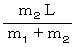 の点 ( W とする ) 上に質量 m1+m2 の物質が存在し物質が存在していることになる。
の点 ( W とする ) 上に質量 m1+m2 の物質が存在し物質が存在していることになる。点Wは2つの物質系の重心である。 ( 物質系とは、 いわば、 物質どうしを質量0太さ0の棒でつないだ剛体である。 だから、 次のトルクのつり合いの式が成り立つ。
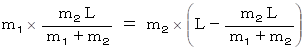
そもそも、 上記の式は、 次の x についての一次方程式を解いて求めたものである。
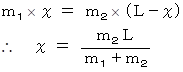
-
点Aの位置ベクトル は A と書くよりも、
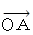 と書くほうがいい。 位置ベクトルの意味が分かりやすいからだ。
と書くほうがいい。 位置ベクトルの意味が分かりやすいからだ。(1) の点Wの位置ベクトル
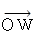 を、 点A と 点B の位置ベクトルを用いて表してみよう。
を、 点A と 点B の位置ベクトルを用いて表してみよう。まず、 次のように書くことができる。
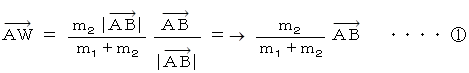
次に、 ベクトルの合成式より、 次の
 と
と  が導かれる。
が導かれる。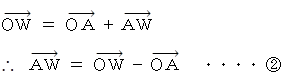
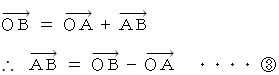
最後に、
 と
と  を
を  に代入して、
に代入して、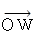 が求まる。
が求まる。
-
(1) のシチュエーションに、 新たに加わるのが、 点C上に存在する質量 m3 の物質である。 3つの物質系の重心の位置ベクトル (
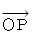 とする ) を、 点A と 点B と 点C の位置ベクトルを用いて表してみよう。
とする ) を、 点A と 点B と 点C の位置ベクトルを用いて表してみよう。まず、 次のように書くことができる。
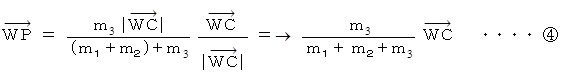
次に、 ベクトルの合成式より、 次の
 と
と  が導かれる。
が導かれる。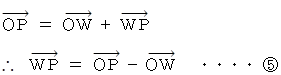
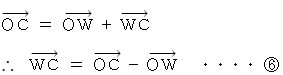
最後に、
 と
と  を
を  に代入して、
に代入して、 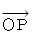 が求まる。
が求まる。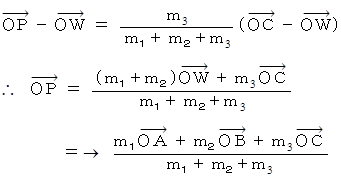
 剛体力学 へ戻る
剛体力学 へ戻る