( 問題1)
-
100人に 0 〜 99 の番号札100枚の中から任意に選んで1枚ずつ配ります。 このとき10の番号札を持っている人が存在する確率はいくらでしょうか?
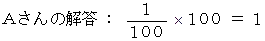
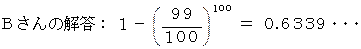
-
正解は、 Aさんです。 誰かが 100分の1 の確率で当選した瞬間に、 必ずその他の人の当選期待値が 100分の1 から0になってしまうような状況に関しては、 Aさんの考え方が正しいのです。
この問題は独立事象ではないケースです。 Aさんが用いた統計学的技法は、 「 X または Y または Z の起こる確率 = X の起こる確率 + Y の起こる確率 + Z の起こる確率 」 ということです。
-
1人が 0 〜 99 の番号札の中から任意に1枚を引いてまた元に戻し、 次の人がまた同じことをします。 100人の人が行った時、 10の番号札を引いた人が存在する確率はいくらでしょうか?
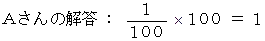
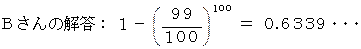
-
正解は、 Bさんです。 誰かが 100分の1 の確率で当選した場合でも、 その他の人の当選期待値がその影響を全く受けないような状況に関しては、 Bさんの考え方が正しいのです。
この問題は独立事象のケースです。 Bさんが用いた統計学的技法は2つです。 「 独立事象においては、 それらが同時に起こる確率は、 1つ1つが起こる確率の積で表される。」 ということと、 「 確率 = 1 − 余事象の確率 」 ということです。
-
100人の人に 0 〜 99 の番号札100枚の中からアットランダムに選んで 1 枚ずつ配ります。 再び回収して、 もう一回同じことをします。 このとき、 2回とも同じ番号だった人が存在する確率はいくらでしょうか?
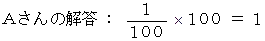
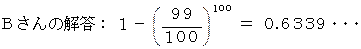
-
正解はBさんのように思われがちですが、 2人とも間違っています。 この問題では、 誰かが 100分の1 の確率で当選した瞬間に、 必ずその他の人の当選期待値が 100分の1 から0になってしまうような状況ではありませんので、 Aさんの考え方が間違っていることは明白です。 またこの問題では、 誰かが 100分の1 の確率で当選した瞬間に、 その他の人の当選期待値が 100分の1 から 99分の1 に上昇しますので、 その影響を全く受けないような状況ではありません。
まず3人のケースで考えてみましょう。 3人に1〜3の赤色番号札3枚の中から任意に選んで1枚ずつ配ります。 続いて1〜3の黒色番号札3枚の中から任意に選んで1枚ずつ配ります。 このとき、 2枚の札の番号が同じ人が1人以上存在する確率はいくらでしょうか?
赤色番号札1をもらった人をAさん、 赤色番号札2をもらった人をBさん、 赤色番号札3をもらった人をCさんとします。 青色番号札の配布の場合の数は次のようになります。
青色番号札1 青色番号札2 青色番号札3
ケース1 Aさん Bさん Cさん
ケース2 Aさん Cさん Bさん
ケース3 Bさん Aさん Cさん
ケース4 Bさん Cさん Aさん
ケース5 Cさん Aさん Bさん
ケース6 Cさん Bさん Aさん
2枚の札の番号が同じ人が1人以上存在するケースは、 ケース1、 ケース2、 ケース3、 ケース6 の4ケースです。 したがって、 2枚の札の番号が同じ人が1人以上存在する確率は3分の2です。
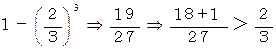
このような問題は、 「 席替えをしたときに、 1人でも元の席と同じ席になる確率はいくらですか?」 という問題と同じであり、 その解答は次の式で与えられるとのことです。
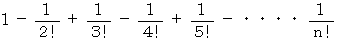
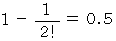
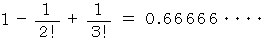
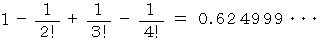
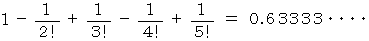
 が無限大の時は、 次のようになります。
が無限大の時は、 次のようになります。
ちなみに、 次のような式が成り立って言いますので、 無限大の人たちが ( 問題3 ) を行うのであれば、 Bさんの考え方も正しいことになります。
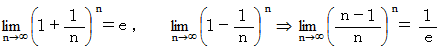
このような問題と解答を考えた人は1700年ころに活躍したモンモールという人らしいです。 この解答を導くのは容易ではありませんので、 せめて、 次のような十進BASIC のプログラムを組んでシュミレーションしてみましょう。
-
n 人のクラスが席替えをします。 無作為に行ったとき、 元の席と同じになる人の数の期待値は?
-
ある1人の人について言えば、 元の席と同じになる確率は 1 / n です。 クラスのみんな 「 同様に確からしい 」 ので、 答えは次のようになります。
答え : ( 1人 × 1 / n )× n =→ 1人
 確率 へ戻る
確率 へ戻る