皆さんこんにちは。鏡に映った文字は、右と左が反対になっているけれど、上と下は反対にはなっていません。今日はその理由をお話ししたいと想います。
その前に、みなさんに想像してほしいことがあります。もし、私の後ろの壁が全部鏡だったとしたら、どんな風景が見えますか? あなたの顔が見えますね。それから他の人の顔も見えます。鏡の中の空間の手前の方には、最前列の人たちが大きく映っています。鏡の中の空間の奥の方には、後ろの座席の人たちが小さく映っています。
では、私の方を向いてください。最初にお断りをしておかなければならないことがあります。それは演題の質問には「鏡を正面視した場合」という条件があるといことです。鏡を正面視するとは、鏡の面に対して垂直な方向から観察するということです。
斜めにして持った本に、鏡を直角に接触させて、文字を上下反転させてみせる。
ご覧のように、鏡を斜めから見ると、上下反転させることができます。また、2つの鏡を上下に三面鏡のように斜めに向かい合わせて見ても、顔が上下逆さまに映ります。
というわけで、今日の演題を少し訂正しなければなりません。今日の演題は、正確には「平面鏡を正面視した場合、なぜ鏡は左右反転させるが上下反転させないのか?」ということになります。この演題に対してなにか異議のある方はありませんか? もしこの演題に違和感を持たれる方があるようでしたら、鏡に映った文字を想像してみてください。
まず最初に思いつく答えは、人間の目が左右に2つ付いているからであり、もし上下に2つ付いていたら「鏡は上下反転させるが、左右反転させない。」ということになりはしないか? ということです。しかし、片目をつむって見ても、鏡は左右反転させるが上下反転させていません。ということで、この考え方は間違いであることがわかります。
私は20年前に床屋(理髪店)で大発見したことがあります。鏡に映ったテレビのホームドラマの映像です。みんな左手で箸を持って食事しているので、一瞬あれっと思いましたが、すぐに「ああそうか鏡に映ってるんで左手で箸を持ってるんだな。」と納得しました、大発見はその後です。鏡に映っている時計が左右反転していなくて普通に映っているのです。不思議な感覚になりました。散髪が終わって、実物の時計を見て納得。それは床屋さん用に作られた反対回りの時計だったのです。
それから5年くらいして、本屋で立ち読みをしていたら、今日の演題に出会いました。その本には、まだその理由は解明されていないと書かれていました。そんなばかなと思いましたが、それからときどき考えました。しかし、「解かった!」と思ってしばらくすると、解かってなかったことが判ります。こうして、ない頭を使って苦節15年、この度やっとこの質問の答えが分かったのです。
解答を申し上げる前に、私の解答の説明を理解しやくするために、4つのお話をさせていただきます。
1番目の話は、鏡に映るものを 自分自身の姿 と それ以外の物 との2つに区別して考えるといいということです。自分自身の姿については、「鏡は左右反転させている」と考える人もあれば、「鏡は左右反転も上下反転もしていない」と考える人もあります。どちらが正しいかは後で述べます。
2番目の話は、「反転は3次元で考えなければならない。」ということです。数学における平面での左右反転や上下反転は2次元の反転ですが、現実は机上の数学とは違います。現実の左右反転や上下反転には、前後反転が隠れているのです。そのことを立方体を自転させることによって実感してみましょう。
立方体の実験:
※ 私にとって手前側の面は「後面」であり、向こう側の面が「前面」になります。これは、
あなた方の立場に立っているのではなく、私自身の座標系においてそう言っているだけです。
1番目の反転です。鉛直な軸を中心に立方体を180°自転させると、
前面と後面が入れ替わり、左面と右面が入れ替わります。
これは「前後反転かつ左右反転」です。
上下の面は同じ平面上で回転します。
2番目の反転です。左右に水平な軸を中心に立方体を180°自転させると、
前面と後面が入れ替わり、上面と下面が入れ替わります。
これは「前後反転かつ上下反転」です。
左右の面は同じ平面上で回転します。
3番目の反転です。前後に水平な軸を中心に立方体を180°自転させると、
上面と下面が入れ替わり、左面と右面が入れ替わります。
これは「上下反転かつ左右反転」です。
前後の面は同じ平面上で回転します。
以上より、立方体を反転させると、必ず2方向の反転が同時に起こることが分りました。
さて、立方体の前面に書かれた図-1 の絵は、
図-1
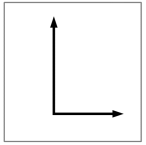
立方体を1番目の反転( 鉛直な軸を中心とする前後反転かつ左右反転 )させると、
同じく前後反転かつ左右反転します。( 立方体が透明だと思って見てください。)
立方体を2番目の反転( 左右に水平な軸を中心とする前後反転かつ上下反転 )させると、
同じく前後反転かつ上下反転します。( 立方体が透明だと思って見てください。)
立方体を3番目の反転( 前後に水平な軸を中心とする上下反転かつ左右反転 )させると、
同じく上下反転かつ左右反転します。
絵が上下反転かつ左右反転するとは、絵が180°回転するということです。
3番目の話は、「物事を観察するときには、観察される物と観察者との相対的な関係の中で考えなければならない。」ということです。例えば、移動している物質があるとします。もし、これを移動している物質と同じ速さで移動している別の観察者が見たらどうでしょう? その物質は静止していることになります。
私たちは顔面に3次元の座標軸を持っていると考えると、観察される物と観察者との相対的な関係が明確になります。喉から頭頂に向かう上下軸、左耳から右耳に向かう左右軸、そして後頭部から眉間に向かう前後軸です。 前後軸の正の方向(前側)にあって、原点から比較的近い所( 手前の方 )が「比較的後ろ側」で、原点から比較的遠い所が「比較的前側」になります。これはマラソンをしている人が自分のすぐ前を走っている手前の方の選手よりもずっと奥の方を走っている選手のほうが前にいると認識するのと同じです。
今から私は振り返ります。すると、私の座標系は前後反転かつ左右反転しました。
今から私は股覗きをします。すると、私の座標系は前後反転かつ上下反転しました。
観察される物は動かなくても観察者の座標系が前後反転かつ上下反転したら、観察者からすると、観察者は動かなくて、観察されるものが相対的に前後反転かつ上下反転したことになります。ですから、股覗きをすることは、観察する物を前後反転かつ上下反転させたことになります。
4番目の話は、「反転には5種類ある」ということです。
1つ目は、「下着を裏返しに着る」に代表される 外面と内面の入れ替え です。
2つ目は、先ほど立方体を使って紹介しました 自転による反転 です。私はこれを「局所空間的反転」と言ってます。
3つ目は、「太陽の相対的公転( 太陽が地球の周りを回っている )」のような、観察者の自転による相対的な反転です。観察者の自転による相対的な反転は、観察者の座標軸を中心にして、同じ向き同じ速さの公転と自転をする物が180°回転したのと同じことです。( 立方体を手に取って自分の周りを同じ面を向けたまま公転させてみる ) 私はこれを「局所空間的反転」に対して「全空間的反転」と言ってます。
4つ目は、写真に映った自分の反転 です。前後反転かつ左右反転しています。それは、自分に向き合っている相手の座標系への変換による反転ですから、私はこれを「座標変換的反転」と言っています。
5つ目は、鏡による反転 です。鏡の中の空間の奥の方にある物ほど、観察者の座標系において、後ろ側の遠い所に存在する物になります。そうです、「鏡反転」は前後反転です。
「もう答えが分かった」という方がいらっしゃるかと存じますが、いよいよ「平面鏡を正面視した場合、なぜ鏡は左右反転させるが上下反転させないのか?」の解答を発表させていただきます。
枠の中の文章をゆっくりと朗読する。
私たちは鏡に映った物をを見たとき、「位置認識」においては左右反転していないと判断し、「画像認識」においては左右反転していると判断します。アクリル板に右矢印(→)を書き、鏡を背にして立ち、自分の右前方に右矢印(→)が見えるようにしてアクリル板を固定します。その後、鏡の方を向いて矢印の鏡像を見ます。それは自分の左後方にあり、左矢印(←)になっています。「左後方にある」というのが位置認識であり、「左矢印(←)である」というのが画像認識です。位置認識に関しては「自分が反転したために、矢印の位置が右前方から左後方に移ったのだ。鏡に映る矢印は、実物の矢印と同じ左後方にある。」と正しく認識できます。しかし、画像認識に関しては「鏡のせいで矢印の向きが 右矢印(→)から 左矢印(←)になっている。」と間違って認識します。矢印の代わりに文字が書かれている場合は特に間違えます。本当は「矢印が左右反転したのは、自分の観察座標系が左右反転したせいだ。鏡に映る矢印は実物の矢印と同じ左向きなのだ。」なのですが。
「位置認識」と「画像認識」の違いがどこから来るかと言うと、私たちは、「位置認識」においては「今の鏡像と今の実像を比較する」のですが、「画像認識」においては「今の鏡像と過去の実像を比較する」ことに由来します。過去の実像とは、鏡に映る前に自分が正面視したときの画像のイメージのことです。 文字が書かれたアクリル板を持って鏡の前に立ってください。鏡は上下反転も左右反転もせずそのまま文字を映し出しています。「位置認識」においては、食うか食われるかの今現在が大切です。一方、「画像認識」においては、正確なイメージが大切なので、落ち着いて正面視した時のイメージを引き合いに出してくるのです。
同様に、私たちは「なぜ鏡は自分の姿を左右反転のみするのだろう?」といった間違った疑問を持つ傾向にあります。その理由は異なる座標系で見たものを比較することに因ります。「自分の座標系における鏡の中の自分」を「自分の座標系における実物の自分」と比較すべきところを、「鏡に映った自分」と「写真に撮られた自分( 向き合っている他人から見られた自分 )」とを比較して間違ってしまうのです。つまり、「自分の座標系における鏡の中の自分」を「向き合っている他人の座標系における実物の自分」とを比較して間違った疑問を持つのです。
「位置認識」と「画像認識」の違いがどこから来るかと言うと、私たちは、「位置認識」においては「今の鏡像と今の実像を比較する」のですが、「画像認識」においては「今の鏡像と過去の実像を比較する」ことに由来します。過去の実像とは、鏡に映る前に自分が正面視したときの画像のイメージのことです。 文字が書かれたアクリル板を持って鏡の前に立ってください。鏡は上下反転も左右反転もせずそのまま文字を映し出しています。「位置認識」においては、食うか食われるかの今現在が大切です。一方、「画像認識」においては、正確なイメージが大切なので、落ち着いて正面視した時のイメージを引き合いに出してくるのです。
同様に、私たちは「なぜ鏡は自分の姿を左右反転のみするのだろう?」といった間違った疑問を持つ傾向にあります。その理由は異なる座標系で見たものを比較することに因ります。「自分の座標系における鏡の中の自分」を「自分の座標系における実物の自分」と比較すべきところを、「鏡に映った自分」と「写真に撮られた自分( 向き合っている他人から見られた自分 )」とを比較して間違ってしまうのです。つまり、「自分の座標系における鏡の中の自分」を「向き合っている他人の座標系における実物の自分」とを比較して間違った疑問を持つのです。
というわけで、答えが分かりました。演題の質問自体が間違っていたのです。鏡は、上下反転も左右反転もさせません。鏡は前後反転のみさせるのです。その証拠に鏡の前に立って右手を振ってください。あなたの座標系において、あなたは前後軸の前方を向いていますが、鏡の中のあなたはあなたの前後軸の後方に向かって、右手を振っています。あなたの左右軸の右側で。
対面している相手が見る自分は、
自分の座標系での自分に対して 前後反転かつ左右反転しています。
それは、自分の座標系に対して 相手の座標系が 前後反転かつ左右反転しいるからです。
自分が撮られた写真を正面から見れば、
自分の座標系での自分に対して 前後反転かつ左反転転しています。。
自分が撮った写真は、反転していません。
平面鏡の面に垂直な方向から鏡を見れば、鏡に映った物は前後反転のみしています。
文字が書かれたアクリル板を持って鏡の前に立ちます。
アクリル板を鉛直な軸を中心にして180°回転させます。それは前後反転かつ左右反転です。鏡は左右反転された文字を左右反転せずにそのまま映しています。左右反転させたのは鏡でなくてあなたです。鏡はアクリル板の文字を前後反転しているだけです。
アクリル板を左右に水平な軸を中心にして180°回転させます。それは上下反転かつ前後反転です。鏡は上下反転された文字を上下反転せずにそのまま映しています。上下反転させたのは鏡でなくてあなたです。鏡はアクリル板の文字を前後反転しているだけです。
鏡を背にして文字が書かれた紙が貼り付けられている壁の前に立ちます。
回れ右をして鏡の方を向きます。それは文字の相対的な前後反転かつ左右反転です。鏡は左右反転された文字を左右反転せずにそのまま映しています。左右反転させたのは鏡でなくてあなたです。鏡は壁に貼り付けられた文字を前後反転しているだけです。
股覗きして鏡を見ます。それは文字の相対的な前後反転かつ上下反転です。鏡は上下反転された文字を上下反転せずにそのまま映しています。上下反転させたのは鏡でなくてあなたです。鏡は壁に貼り付けられた文字を前後反転しているだけです。
というわけで、私が本日皆さんにお伝えしたかったことは次のことだったのです。
「平面鏡を正面視した場合、なぜ鏡は文字を左右反転させるが上下反転させないのか?」という質問は、質問自体が間違っています。鏡は前後反転させるだけです。鏡に本の表紙を映す前に、観察者は自分の方を向いていた本の表紙を鏡の方へ向けます。つまり、本を前後反転かつ左右反転させます。そして観察者は「反転させる前の本の表紙の文字」と「反転させた後に鏡に映っている本の表紙の文字」とを比べて「鏡は文字を左右反転させる」と思ってしまうのです。しかし、比べなければならないのは 「 観察者の座標系における鏡に今映っている本の表紙の文字 」 と 「 観察者の座標系における今実際に存在する本の表紙の文字 」 です。
「平面鏡を正面視した場合、なぜ鏡は自分の姿を左右反転させるが上下反転させないのか?」という質問は、質問自体が間違っています。鏡は前後反転させるだけです。私たちは「鏡に映った自分」と「写真に撮られた自分( 向き合っている他人から見られた自分 )」とを比べて「鏡は自分の姿を左右反転させる」と思ってしまいがちです。しかし、比べなければならないのは 「自分の座標系における鏡の中の自分」と「自分の座標系における実物の自分」です。
2つの物を比べるときには、
同じ座標系で比べなければなりません。
同じ時刻に比べなければなりません。
「平面鏡を正面視した場合、なぜ鏡は自分の姿を左右反転させるが上下反転させないのか?」という質問は、質問自体が間違っています。鏡は前後反転させるだけです。私たちは「鏡に映った自分」と「写真に撮られた自分( 向き合っている他人から見られた自分 )」とを比べて「鏡は自分の姿を左右反転させる」と思ってしまいがちです。しかし、比べなければならないのは 「自分の座標系における鏡の中の自分」と「自分の座標系における実物の自分」です。
2つの物を比べるときには、
同じ座標系で比べなければなりません。
同じ時刻に比べなければなりません。
まだ少し時間がありますので、最後に「反転の合成」についてお話させていただきます。
左右反転、上下反転、前後反転は、それぞれ合成されます。合成の結果、反転が偶数倍になれば反転のない状態になり、反転が奇数倍になれば反転のある状態になります。
鏡を背にして立ち景色を観察します。その後回れ右をして、鏡に映る景色を見ます。景色は左右反転しています。あなたによって景色は前後反転+左右反転させられました。鏡によって景色は前後反転させられました。鏡は合計で 2×前後反転+左右反転 させられました。ということは、結局、景色は左右反転のみさせられたことになります。
ご清聴ありがとうございました。
練習問題:
-
図-1 の絵が書いてあるアクリル板を持って立ちます。次に、アクリル板を鉛直な軸を中心に前後反転かつ左右反転させます。その次に、今のアクリル板を持った自分の姿を誰かに頼んで写真に撮ってもらいます。その次に、出来上がった写真を持って鏡の前に立ちます。その次に、写真を左右の水平な軸を中心に前後反転かつ上下反転させます。このとき、鏡に写っている写真の中の 図-1 の絵は一番最初に見た状態からどのような反転をしていますか?
-
上下反転
-
(前後反転+左右反転)+(前後反転+左右反転)+(前後転反+上下反転)+前後反転
=→ 4×前後反転 + 2×左右反転 + 上下反転
=→ 上下反転
 数学と物理学 へ戻る
数学と物理学 へ戻る