【 問 題 １ 】

　ボタンを押すと、０から 10 までの実数を無作為に１つ表示してくれる器械があります。100回ボタンを押して表示された数の平均をとることにします。平均値の期待値はいくらでしょうか？

【 解 答 】

1 回ボタンを押して表示された数を y とすると、x ＜ y ＜ x ＋ dx である確率は　1×dx / 1×10　だから、
　　　
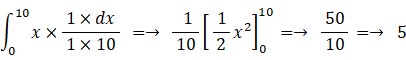
　　　　　　　　　※ 参照： 大学生のための数学 ＞ 解析学 ＞ ある積分の意味

【 問 題 ２ 】

　ボタンを押すと、０から 10 までの実数を１つ表示してくれる器械があります。この器械は、表示する数の大きさに比例してその数が表示される確率が高くなっています。100回ボタンを押して表示された数の平均をとることにします。平均値の期待値はいくらでしょうか？

【 解 答 】

1 回ボタンを押して表示された数を y とすると、x ＜ y ＜ x ＋ dx である確率は　x×dx / ( 1/2×10×10 )　だから、
　　　

【 問 題 ３ 】

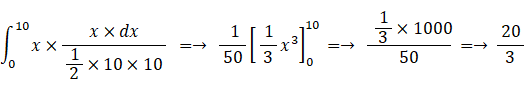
　薄くて固い正方形をしたタイル型の太陽光発電器があります。一辺の長さは１メートルです。表側を太陽光（ エネルギーは一定とします。）に対して垂直に当てたときの発電量を 100 とします。表側に太陽光が直接当たらないときの発電量は 0 です。表側を太陽光に対して斜め45度に当てたときの発電量は 100 / root(2) です。
　この太陽光発電器を無作為の姿勢で太陽光に当てたときの発電量の期待値を求めなさい。

【 解 答 】

　1/2 の確率で発電量は 0 になる。 これから 発電量 ＞ 0 の場合について考える。
　太陽光発電器の表側に大きさ１の法線ベクトルを考える。法線ベクトルと逆太陽光ベクトルとが作る角を θ ラジアンとすると、 0 ≦ θ ＜ π/2　という不等式が成り立つ。
　θ ＝ α のとき、太陽光発電器を重心を通る法線ベクトルを中心にいくら自転させても、太陽光発電器に太陽光の当たる面積や角度は一定である。したがって、θ ＝ α のとき、太陽光発電器の発電量は 100×cosα になる。
　θ ＜ α ＜ θ＋dθ である確率は　2πsinθ×dθ / ( 1/2 × 4π )　だから、
　　　　　　　　　　　※　2πsinθ は 半径 sinθ の円の円周の長さ
　　　　　　　　　　　※　4π は 半径 1 の球の表面積
発電量の期待値は次のようになる。
　　　
　　　　　　　　　　　
　　　　　　　　　　　
　　　　　　　　　　　
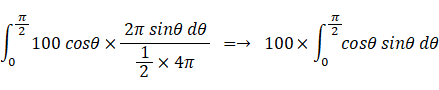
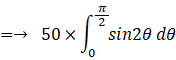
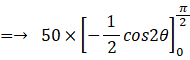
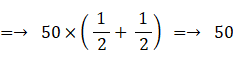
以上にて、 発電量 ＞ 0 の場合についての考察は終了した。
したがって、求める答えは次のようになる。
　　　0 × 1/2 ＋ 50 × 1/2　＝→　25