【 問 題 】
-
傾斜角 10度 の坂道に質量 m kg 半径 r m の円筒をそっと置いたところ、滑ることなく転倒回転を始めた。その後、自然に回転走行も加わり、円筒は自転しながら高い方から低い方へと移動していった。では、高さが出発点よりも h m 低い位置になったときの円筒の移動速度の大きさ( v m/s )を求めなさい。
なお、
-
重力加速度 = g m/s2 としなさい。
半径 r m の円筒の慣性モーメント( I ) は I = m r2 kgm2 である。
転がり摩擦や回転走行摩擦によって音や熱は発生しないものとする。
空気抗力は0とする。
-
力学的エネルギー保存側より、
mgh = 1/2 × m × v2 + 1/2 × I × ω2
= 1/2 × m × v2 + 1/2 × m r2 × v2/r2
よって、
v = root ( gh ) ( m/s )
以上が答えですが、もしこの円筒が全く転がらずに滑り落ちた場合には、これよりも root ( 2 ) 倍速くなります。
【 解説 】
-
全く滑ることなく転がり落ちるときの力学的エネルギー保存側:
mgh = 1/2 × m × v2 + 1/2 × I × ω2
= 1/2 × m × v2 + 1/2 × I × v2/r2
= 1/2 × m × v2 + 1/2 × I/r2 × v2
= 1/2 × ( m + I/r2 ) × v2
※ 私は次のパラメーターを 「 移動慣性量 」 と言っています。
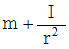
>
 剛体力学 へ戻る
剛体力学 へ戻る