（１）　x 軸を中心とする回転体の体積と面積

　　　　　　　　　　　　　

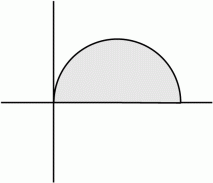
　 区間 0 〜 x において 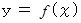と x 軸によって囲まれる部分を x 軸を中心として 360度回転してできる立体の体積と表面積を求めてみましょう。

その立体の微小区間 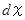おいては、
　　　　微小体積 ：　
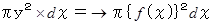
　　　　微小表面積 ：　
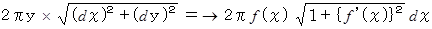
これらをアナログ的に総計して、
　　　　求める体積　＝　
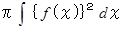
　　　　求める表面積　＝　


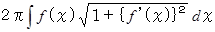
　 具体例として、 半径 ｒ の球の場合を考えましょう。
　 区間 x ＝ 0 〜 2ｒ の第１象限に存在する x 軸上に中心がある半径 ｒ の半円を回転してできる球の場合です。
　　　　
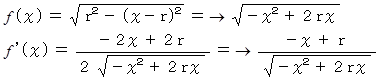
半径 ｒ の球の体積 ：
　　　　
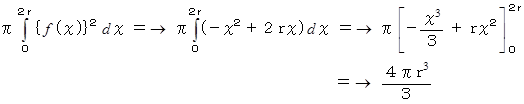
半径 ｒ の球の表面積 ：
　　　　

（２）　y 軸を中心とする回転体の体積 （ バウムクーヘン分割積分 ）

　　　　　　　　　　　　　

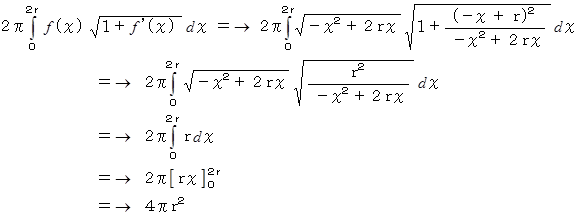
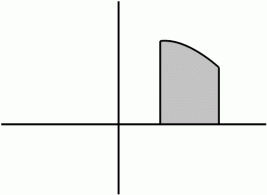
　 　と　x 軸 とで囲まれる部分を y 軸中心に回転させてできる立体の体積は、 「 バウムクーヘン分割積分 」 によって求めることができます。
　 この方法は、 立体をバウムクーヘンの層のように無数に分解し、 展開した長方形的直方体 （ カンナで削られた極薄い板 ） の　面積 × 微小厚さ ＝ 微小体積　を無数に加えて求める方法です。

　　　　展開した長方形の面積の横の長さ　＝　2πx
　　　　展開した長方形の面積の縦の長さ　＝　
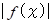
　　　　展開した長方形の微小の厚さ　＝　

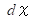
したがって、 回転体の体積は
　　　　

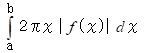
例 ：
　　　　

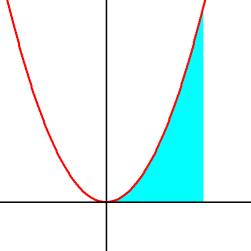
　赤色の曲線は y ＝ x ² で表される放物線です。 水色で塗られた部分は　0 ≦ x ≦ 2　の範囲になります。
　水色で塗られた部分を y 軸を中心に 360 度 回転させてできる回転体の体積を求めましょう。
　　　　

（３） パップスギュルダンの定理

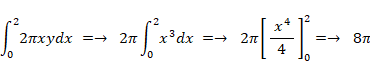
　2 ≦ x ≦ 4　かつ　0 ≦ y ≦ 2　は２次元直交 x y 座標系のある場所に存在する正方形を表します。この図形を y 軸を中心にして 360 度回転してできる回転体の体積（ V ）は次のようになります。
　　　V ＝ ( 2 × 2 ) × ( 2π × 3 )　＝→　24π
( 2 × 2 ) は 正方形の面積 で、 ( 2π × 3 ) は 正方形の重心を 360 度回したときの道のり です。パップスギュルダンの定理は、バウムクーヘン分割積分を 重心の回転軸からの距離 を用いて表したものです。