(1) カイ2乗検定による適合度検定
( 問い 1 )
均一な密度でできた立方体は重心が中心にありますので、 放り投げた後に床を転がって静止すると、 ある面が上にある確率はすべて6分の1になります。 あるサイコロを100回振ったときに、 奇数が58回、 偶数が42回 出ました。 このサイコロは丁半で使用することができるでしょうか?
-
奇数
偶数
計
このサイコロ
58
42
100
-
帰無仮説 : 「 このサイコロは、 奇数と偶数が半々に出る。」
帰無仮説に従った理想表:
奇数
偶数
計
理想のサイコロ
50
50
100
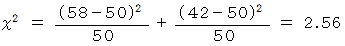
カイ2乗分布表を見ると、 自由度1で有意水準( 危険率 )
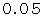 の場合は、
の場合は、 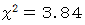 になっています。
になっています。  ですから、 帰無仮説を棄却できません。 ということは、 危険率 5%では、このサイコロは丁半で使用することができないと言い切ることはできません。
ですから、 帰無仮説を棄却できません。 ということは、 危険率 5%では、このサイコロは丁半で使用することができないと言い切ることはできません。( 問い 2 )
では、 100回振ったときに、 奇数が60回、 偶数40回 出たサイコロは、丁半で使用することができるでしょうか?
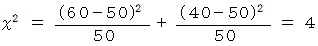
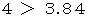 ですから、 帰無仮説を棄却することができます。 ということは、 危険率 5%で、このサイコロは丁半で使用することはできないと言い切れます。
ですから、 帰無仮説を棄却することができます。 ということは、 危険率 5%で、このサイコロは丁半で使用することはできないと言い切れます。(2) カイ2乗検定による独立性検定
( 問い 3 )
あるラグビーチームの過去100回の成績を天候別にみたところ、 雨の日の勝率は
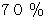 で、 雨以外の日の勝率は
で、 雨以外の日の勝率は 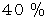 でした。 このチームは雨に強いと言えるでしょうか?
でした。 このチームは雨に強いと言えるでしょうか?帰無仮説 : 「 雨の日の勝率 と 雨以外の日の勝率 とには、 優位差は無い。」
-
勝ち
負け
計
雨の日
14
6
20
雨以外
32
48
80
計
46
54
100
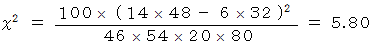
カイ2乗分布表を見ると、 自由度1で有意水準
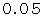 の場合は、
の場合は、 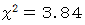 になっています。
になっています。  ですから、 帰無仮説を棄却することができます。 ということは、 危険率 5%で、このラグビーチームは雨の日の勝率が明らかに高いといえます。
ですから、 帰無仮説を棄却することができます。 ということは、 危険率 5%で、このラグビーチームは雨の日の勝率が明らかに高いといえます。 統計学 へ戻る
統計学 へ戻る