確率 へ戻る正三角形の一辺の長さは、内接円の半径の
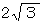倍であり、外接円の半径の 
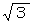倍です。
【 問 題 】
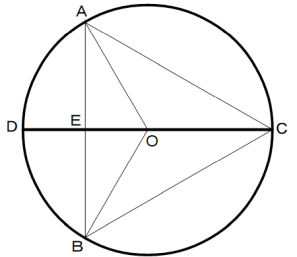
中心を点Оとする円に正三角形ＡＢＣが内接している。
中心を点Оとする円に正三角形ＡＢＣが内接している。
-
（１） 円周上に無作為に２点を取りそれを結ぶ直線を描く。
その直線が円の内部を通る長さが正三角形ＡＢＣの一辺の長さ以上になる確率を述べよ。
（２） 円の直径ＤＣ上に無作為に１点を取り、その点を通りＤＣに垂直な直線を描く。
その直線が円の内部を通る長さが正三角形ＡＢＣの一辺の長さ以上になる確率を述べよ。
-
（１） １点を取った後に、２つ目の点の位置によって結果が決まる。
したがって、最初の点の取り方は確率に全く影響を与えない。
そこで、最初に点Ａを取ることにする。
このとき、２つ目の点が弧ＢＣ上にあるときに、 求める事象となる。
したがって、求める確率は 1/3 である。
（２） 無作為に取るＤＣ上の点の点Оからの距離がＥＯの長さ以内であれば求める事象となる。
ＤＥ ＝ ＥＯ だから、求める確率は 1/2 である。
以上の問題は、「 無作為に円の内部を通過する直線を引いたときに、その直線が円の内部を通る部分の長さが円の半径の
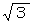倍以上になる確率を求めよ。ただし、無作為といっても、ある条件に従って直線を引く場合である。」ということです。そこで今度は、条件なしの本当に無作為の場合について考えてみましょう。
＜ 無条件下での無作為的選択方法 ＞
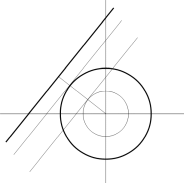
「中心が原点に存在する半径１の円の内部を通過する直線を無作為に１つ選んでその方程式を書け。」という命令に従うには、直線 y ＝ a x ＋ b が中心が原点に存在する半径１の円の内部を通過するようにさせる a と b の組み合わせの中から無作為に１つを選べばいい。直線 y ＝ a x ＋ b の原点からの距離が１未満であるとき、直線 y ＝ a x ＋ b は中心が原点に存在する半径１の円の内部を通過する。直線 y ＝ a x ＋ b の原点からの距離は次の式で表される。
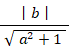参照： 図形の方程式 ＞ 点から直線までの距離
したがって、直線 y ＝ a x ＋ b が中心が原点に存在する半径１の円の内部を通過するためには、次の式が成り立てばよい。
つまり、
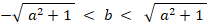・・・・ ①
この条件を満たす a と b のペアを１組作るには、まず、a を －∞ 以上 ＋∞ 未満 の範囲から１つ選び、その次に b を①の範囲から１つ選べばいい。このとき、もし b が次の範囲内にあれば、直線が円の内部を通る部分の長さが円の半径の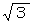 倍以上になっている。
つまり、
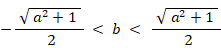・・・・ ②
①の範囲内にある b の値の中から無作為に１つだけ選んだ場合、それが②の範囲内にある確率は 1/2 である。したがって、無条件下の無作為に円の内部を通過する直線を引いたとき、その直線が円の内部を通る部分の長さが円の半径の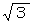 倍以上になる確率は 1/2 であることが分かった。
「中心が原点に存在する半径１の円の内部を通過する直線を無作為に１つ選んでその方程式を書け。」という命令に従うには、直線 y ＝ a x ＋ b が中心が原点に存在する半径１の円の内部を通過するようにさせる a と b の組み合わせの中から無作為に１つを選べばいい。直線 y ＝ a x ＋ b の原点からの距離が１未満であるとき、直線 y ＝ a x ＋ b は中心が原点に存在する半径１の円の内部を通過する。直線 y ＝ a x ＋ b の原点からの距離は次の式で表される。
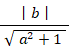参照： 図形の方程式 ＞ 点から直線までの距離したがって、直線 y ＝ a x ＋ b が中心が原点に存在する半径１の円の内部を通過するためには、次の式が成り立てばよい。
つまり、
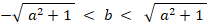・・・・ ①この条件を満たす a と b のペアを１組作るには、まず、a を －∞ 以上 ＋∞ 未満 の範囲から１つ選び、その次に b を①の範囲から１つ選べばいい。このとき、もし b が次の範囲内にあれば、直線が円の内部を通る部分の長さが円の半径の
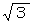倍以上になっている。つまり、
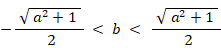・・・・ ②①の範囲内にある b の値の中から無作為に１つだけ選んだ場合、それが②の範囲内にある確率は 1/2 である。したがって、無条件下の無作為に円の内部を通過する直線を引いたとき、その直線が円の内部を通る部分の長さが円の半径の
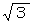倍以上になる確率は 1/2 であることが分かった。でも、ここで問題です。円の内部を通る直線は、円周の上の２点を通ります。円周上の２点を最初に決めてから直線を作るのと、最初に直線の傾きを決めてからそれが円周上の２点を通るように上下に平行移動させるのと。前者は条件下の無作為であり、後者は無条件下の無作為である、と言えるのでしょうか？
答えは、「そう言い切ることができる」です。「無作為に円の内部を通過する直線を引く」ということは、「円の内部を通る直線は無数にあるけれど、その中から１本の直線を無作為に選ぶ」ということです。直線の個性とは何かと尋ねたとき、それは傾きと位置であると言うことができます。直線の個性を決めるのは２つの点です。その２点が決まるとそれらを通る直線が１つ決まるからです。2点の決め方には２通りあります。方法その１を紹介します。それは、まず、１点の位置を決めてから、次に残リの点の位置を決める方法です。これは、まず直線の回転中心を決めてから、架空の直線を回転させて傾きを決めるやり方です。方法その２を紹介します。それは、まず、ある点に対するもう一つの点の相対的な位置を決めてから、次に、基準になっている点の位置を決める方法です。これは、まず直線の傾きを決めてから、架空の直線を平行移動させて直線の通る点を決めるやり方です。
無条件下で無作為に直線を１つ選ぶということは、無限の空間の中から無作為に2点を選ぶということです。決められた円周上の点の中からしか選べないというのは、条件下での無作為的選択になります。一方、問題（２）の答えが 無条件下での無作為と同じ 1/2 になるのはなぜかと申しますと、条件下の無作為ではあリますが、実際は無条件下の無作為になっているからです。なぜなら、まず任意に直線の傾きを決めた直後に図形全体を回転させて直線を垂直にしてから、直線が円の内部を通過するようになる範囲内で無作為に直線を水平移動させて１箇所に固定させることと同じだからです。
２つ目の枠の中で述べたことは「無条件下で無作為に１本の直線を選択したときに、それが定められた円の内部を通過する場合において、題意を満たす場合の占める割合を求めること」ですが、そこでは「直線を決定する２点を決める方法その２」を用いています。しかし、方法その１を利用することもできます。ただし、そうするには少し思考の準備体操が必要です。方法その１で直線を無作為に１つ選ぼうとすると、無限に広がる平面の中から１点をまず選択するわけですから、その架空直線の回転中心は平均して原点から果てしもなく離れたところになります。したがって、「そこを通リ原点を中心とする半径１の円に接する直線」と「そこを通リ原点を中心とする半径 1/2 の円に接する直線」とは平行であるとみなすことができます。したがって、「そこを通リ原点を中心とする半径１の円の内部を通過する直線」の中から「そこを通リ原点を中心とする半径 1/2 の円の内部を通過する直線」を選ぶ確率は 1/2 であるとみなすことができるのです。