スイッチを押すと０〜２の範囲の中から１個の数を表示してくれるマシーンがあります。無限回スイッチを押して表示された数（ 確率変数 ）の確率密度分布を調べると、f ( x ) ＝ x/2 ( 0 ≦ x ≦ 2 ）という確率分布関数で表されることが分かりました。
　次に、このマシーンのスイッチを２回押して表示された２つの数の和（ 確率変数 ）を取るということを無限回行ってその確率密度分布を調べました。和が 1 のときの確率密度はいくらになったでしょうか？ また、和が 2 のときの確率密度はいくらになったでしょうか？ また、和が 3 のときの確率密度はいくらになったでしょうか？

　　　

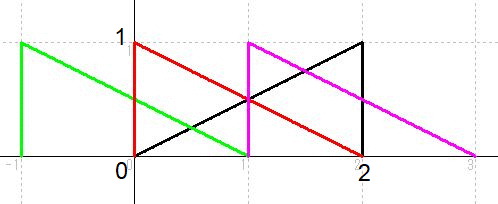
　f ( x )：黒図　　f ( 1−x)：緑図　　f ( 2−x )：赤図　　f ( 3−x )：桃図

　0≦x≦2 の f ( x ) ＝ x/2 の定積分の近似値： 1.000005
　0≦x≦1 の f ( x ) と f ( 1−x ) の内積の近似値： 4.16666666642032 ×10⁻²
　0≦x≦2 の f ( x ) と f ( 2−x ) の内積の近似値： 33.3333333342217 ×10⁻²
　1≦x≦2 の f ( x ) と f ( 3−x ) の内積の近似値： 54.1671666673031 ×10⁻²

　ちなみに、黒図と緑図の重なりの面積 ＝ 1/8 ＝ 0.125
　ちなみに、黒図と赤図の重なりの面積 ＝ 1/2 ＝ 0.5
　ちなみに、黒図と桃図の重なりの面積 ＝ 5/8 ＝ 0.625

　したがって、
　　　　和が 1 のときの確率密度　≒　0.0417
　　　　和が 2 のときの確率密度　≒　0.3333
　　　　和が 3 のときの確率密度　≒　0.5417

十進BASIC のプログラムの内容：

　※　参考：
　　　　　大学生のための数学 ＞ その他の数学 ＞ Desmosで畳み込み
　　　　　大学生のための数学 ＞ その他の数学 ＞ 周期関数の内積