「 椅子が6個一列に並んでいる。 8人の人がいる。 人が6個の椅子すべてに座るとき全部で何通りあるか? ただし、 椅子には 1 人しか着けないものとする。」 という問題の答えは、 一般的には 8P6 です。 なぜなら、 実際には人が席を選んで座るからです。
これを 「 席たちが人を呼び寄せる 」 という発想で展開してみます。 つまり、 席たちを主人公とするのです。 まず、 6人を選ぶ場合の数です。 それは 8C6 です。 そしてそれが決まったら、 席たちが自分に着かせる人を選択していきます。 そのすべての場合の数は 6P6 = 6! です。 したがって、 6個の席が8人の人を呼び寄せるすべての場合の数は 8C6 × 6! です。 8C6 × 6! = 8P6 です。
順列・組み合わせの基本的な式:
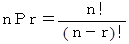
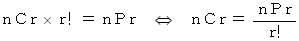
 確率 へ戻る
確率 へ戻る