慣性モーメントの性質：

１．剛体内を貫通する直線を回転軸とする回転では、回転軸により慣性モーメントは異なる。

２．剛体内に座標原点を取って x yｚ３次元座標系を描いたとき、
　　その中のある座標軸を回転軸とする回転の慣性モーメントは、
　　他の２つの座標軸を回転軸とする回転の慣性モーメントの和に等しい。

３．剛体の質量を m kg とする。
　　剛体の重心を通る直線を中心とする回転の慣性モーメントは、
　　その回転軸に平行で q m 離れた剛体を貫く直線を中心とする回転の慣性モーメントよりも
　　 m q² kg/m² だけ小さい。

４．剛体が重心を通る直線を中心とする回転をしながら、移動しているとき、
　　移動の速さを v m/sとし、回転の角速度の大きさを ω rad/s とし、
　　慣性モーメントを Ｉ kg/m² とすると、運動エネルギーは次の式で表される。

　　　　　運動エネルギー　＝　移動エネルギー　＋　回転エネルギー
　　　　　　　　　　　　　

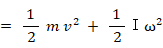
　角運動量原理から回転運動方程式を導いてみましょう。
　回転軸をＺ軸とする３次元座標系を考えます。剛体はＸ軸からＹ軸の方向に角速度の大きさ ω rad/s で回転しているものとします。
　剛体内の微小区域の運動量モーメントの方向はすべてＺ軸の正の方向です。
　剛体を一様な密度としてそれを ρ kg/m³ で表すと、剛体内の微小区域（ 体積 dV m³ ）の質量は 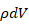kg になります。
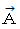　 に 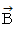を外積させる演算 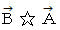（ ） は、 次のように表されます。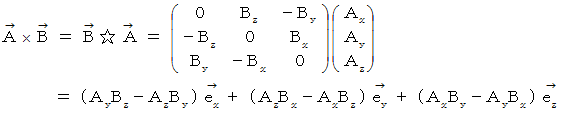
　　　　
運動量モーメントは、 位置ベクトル × 運動量 ですから、剛体内の微小区域の運動量モーメントは次のようになります。
　　　
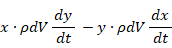
これを円筒座標表示（ ＸＹ平面極座標表示 ）にすると、次のようになります。
　　　
　　　　　　
　　　　　　
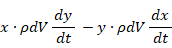
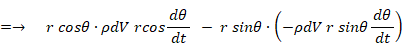
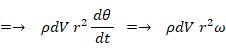
したがって、剛体内の微小区域の運動量モーメントの総和は次のようになります。
　　　
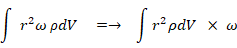
この式を時間で微分すると次のようになります。
　　　
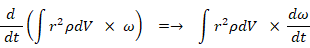
角運動量原理より、上式は、剛体内の微小区域に作用する力モーメントの総和 になっています。
そこで、次のように慣性モーメントを定義します。
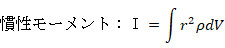　　　　（ 単位は kg・m² ）
こうして、回転運動方程式 が導かれます。