（１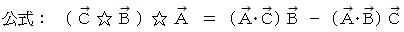） 　の証明

　　　　　　　　　　　　　　　　　　　　　


　
　
　

　

（２） 慣性テンソル

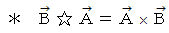
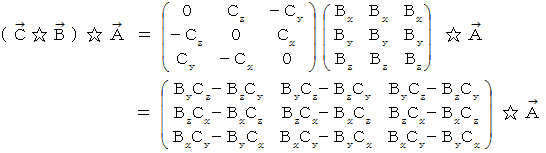
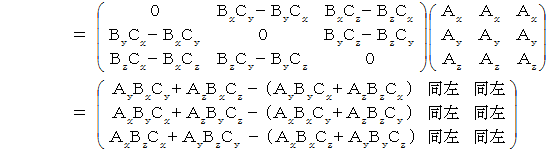
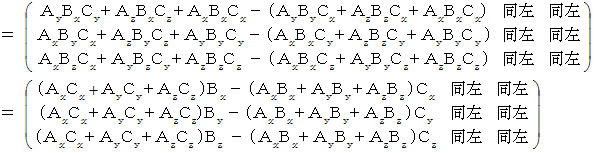
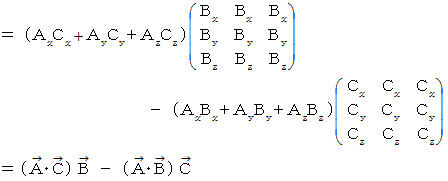
　 剛体がある軸を中心として自転しています。 その軸上の剛体内の１点を原点として からなる３次元直交座標系を設定します。 そして、 この剛体の角速度 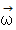と 角運動量 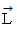をそれぞれ次のように表します。
　　　　
角速度 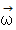の向きは回転軸の向きに平行です。
　 剛体内の微小部分の質点の質量を 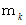とし、 原点から位置ベクトル 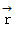を次のように表します。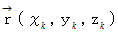
　　　　
すると、 剛体の角運動量は次のようになります。
　　　　
　　　　
　　　　
　　　　
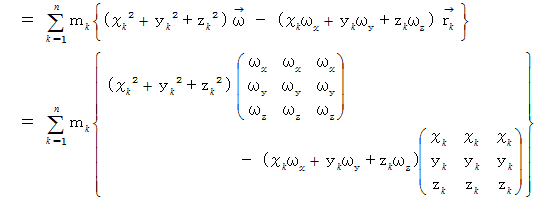
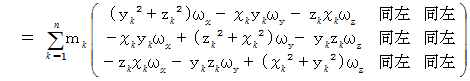
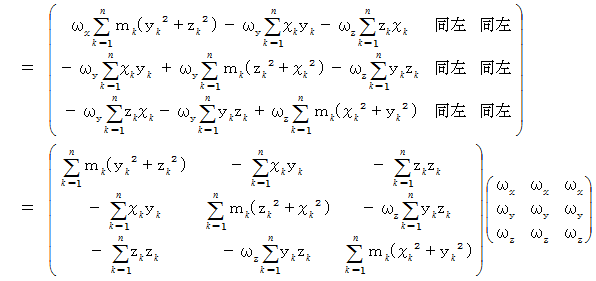
ここで、 次のように置きます。
　　　　
すると、 次のようになります。
　　　　
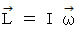
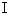は空間的テンソルであり、 その表現行列は対称行列になっています。
　 私たちは、 今まで、 剛体の慣性モーメントをスカラーとして捉えており、 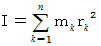と表現してきました。 剛体の慣性モーメントを質点の質量に対応するものと考え、 質点の移動速度のベクトルにスカラーである質点をかけると速度と同じ向きの運動量ベクトルが得られるように、 剛体の角速度にスカラーである慣性モーメントをかけると角速度と同じ向きの角運動量ベクトルが得られると考え、 角速度を 　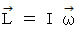と表現してきました。 しかし、 それは自転軸が固定されている拘束回転運動にのみ通じることだったのです。 今回のように自転軸が固定されてなくて自転軸自体が回転するような自由回転運動を考えて解ったことは、 慣性モーメントの正体は慣性テンソルであり、 慣性テンソルは角速度に作用して角運動量を取り出す空間的テンソルであるということです。 慣性テンソルは応力テンソルのような量場的テンソルではありません。 角速度を表す式はこれまでと同じ　　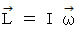ですが、 中身が違います。 したがって、 角運動量 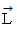の向きは、 剛体の角速度 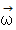の向きと異なり、 剛体の回転軸と異なることがわかりました。

　 さて、 スカラーであるところの質量は、「 慣性質量 」という役割も担っており、 力に作用する演算子として振舞うこともあります。 そこで、 さきほど、 慣性テンソルは空間的テンソルであり量場的テンソルではないという言い方をしましたが、 これは早速訂正しておかなければなりません。 正しくは、「 慣性テンソルは応力テンソルと同様に量場的テンソルであり、かつ、空間的テンソルです。」 そもそも、 空間的テンソル とか 量場的テンソル という言葉は私が勝手に作った言葉です。 あえてこの言葉を使って慣性テンソルについて説明するならば、 慣性テンソルは基本的には量場的テンソルであり、 それは空間的テンソルとして働いていると言うべきだと思います。 その慣性テンソルの働きによって、 剛体は自転しながら自転とは別の回転をするのです。 剛体は力のモーメントが加わらない限り、 これまでの自転軸を中心にして同じ速さで自転し続けます。 しかし、 剛体の持つ慣性テンソルは、 自転軸そのものを回転させるように作用するのです。

　 慣性テンソルの表現行列が対称行列になっているということは、「 対称行列は直交行列によって対角化される 」のだから、 直交座標系の選び方しだいで、 慣性テンソルの表現行列はスカトリオ（ スカトリオも私の造語です ）になるということです。 すると、 角速度から角運動量を導き出すことが簡単になります。 もちろん、 角運動量は角速度と同じ向きではありません。

　 質点の運動量を時間で微分すると質点に作用している力が解るように、 角運動量を時間で微分すると、 剛体に作用している力のモーメントが解ります。 前者は運動方程式で、 後者は回転運動方程式です。