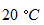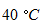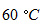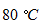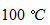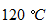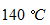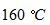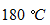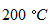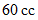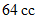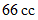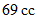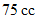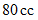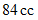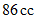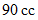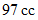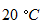ばいおりんの慣性系相対性理論

の気体

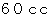を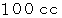

のガラスの注射器に封じ込めて、注射器の内筒の重さが気体に加わるようにして注射器を立て、温度を

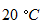ずつ上昇させながら、気体の体積を測定しました。そのときのデーターを次に示します。

　　温度の平均値：　
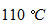
　　体積の平均値：　
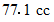
　　温度の分散：　　
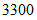
　　体積の分散：　　
　　　　　　　　

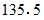
　分散とは平均からの隔たりの２乗の平均のことです。
　　　　　　　　　分散の正の平方根は、標準偏差と言われます。
　　温度と体積の共分散：　
　　　　　　　　

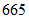
　共分散とは平均からの隔たりの積の平均のことです。
　　　　　　　　　　　※ 参照：大学生のための数学＞統計学＞共分散

　　相関係数 ：　温度と体積の間に相関関係があるかどうか？
　　　　　　　

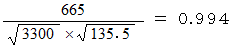
　相関係数はで、絶対値が

に近いほど
　　　　　　　　　　　　相関関係が強いと言えます。

　　回帰直線 ：　相関関係をおおまかに直線（一次方程式）で表したもの。
　　　　　　　

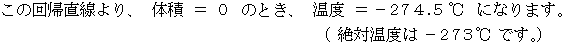
　以上、シャルルの法則（圧力が一定のとき、理想気体の体積は絶対温度に比例する。）を実験より解析して導き出したという、シナリオでした。

　回帰直線とは、すべての標本を２次元直交座標にプロットしたときに、その

軸方向の隔たりの平均が最小になる直線のことです。

上記の２つの式より次の式が成り立ちます。
　　　　

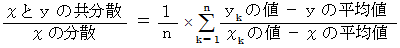
　この式より、

と

の間には、およそ次のような一次式で表される関係式が成り立っていると言うことができます。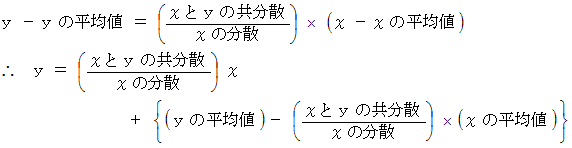
　　　　

これが回帰直線です。

　「回帰直線から求めた完全な相関関係と仮定した場合の修正ｙ座標値」と「各標本の実際のｙ座標値」との隔たりを見ることによって、実際の相関関係がどれくらいの程度なのかを知ることができます。そこで、まず次の式を作ってその指標とすることにします。

　　　　

　　　　したがって、次のようになります。
　　　　　　　　　

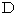は「相関係数」と言われます。相関係数が＋の場合は正の相関に、－の場合は負の相関になっています。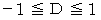であり、一般的には

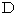の絶対値が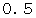

以上のときに相関関係があると考えられます。

　山中和義 / 電脳遊戯団さんが作られた統計関数のプログラムを参考にさせていただき、十進BASIC で、回帰直線や相関係数を求めるプログラムを作ってみました。