【 問 題 １ 】

　 0　〜　2n−1 （ n は自然数 ） の　2n 個の整数を、 ボタンを押すごとに １ 個ずつランダムに表示するマシーンがある。 2回ボタンを押して得られた数をかけ合わせると 0 だった。 ２つの数字とも n−1 以下である確率はいくらか？

　【 解 答 】

( 0, 0 ), ( 0, 1 ), ( 0, 2 ), ( 0, 3 ), ・・・, ( 0, n−1 ), ・・・, ( 0, 2n−1 )
( 1, 0 )
( 2, 0 )
( 3, 0 )
　 ・
　 ・
( n−1, 0 )
　 ・
　 ・
( 2n−1, 0 )


答えは、　( 2×n−1 ) / ( 2×2n−1 ) 　＝→　( 2n−1 ) / ( 4n−1 )

【 問 題 ２ 】

彼女には２人の子供がある。
彼女の子供が２人とも女の子である確率はいくらか？

　【 解 答 】

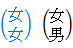
　　　　※ 上段は第１子が 女の子 であるケース。
　　　　※ 下段は第１子が 男の子 であるケース。
　　　　※ 左列は第２子が 女の子 であるケース。
　　　　※ 右列は第１子が 男の子 であるケース。
　　　　※ ４つのケースが存在するのは同様に確からしい。

したがって、答えは 1/4 になる。

【 問 題 ３ 】

彼女には２人の子供がある。
少なくとも１人は女の子である。
彼女の子供が２人とも女の子である確率はいくらか？

　【 解 答 】

「彼女の子供は２人とも男の子であるということはない。」 という情報を得る前だったら、 彼女の子供が２人とも女の子である確率は 1/4 であるが、 その情報を得た瞬間に確率は 1/3 に変化する。

　【 別 解 】

【 問 題 １ 】 の解答に n＝1 を代入して、 1/3 になる。

【 問 題 ４ 】　⇒ 「 火曜日に生まれた女の子のパラドックス 」

彼女には２人の子供がある。
少なくとも１人は火曜日に生まれた女の子である。
彼女の子供が２人とも女の子である確率はいくらか？

　【 解 答 】　　※ ブラウザの画面をを十分に広げてからご覧ください。

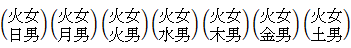
したがって、答えは 13 / 27　になる。
不思議ですね。「 火曜日生まれ 」という情報は性別になんら関係ないのに・・・・。

　【 別 解 】

【 問 題 １ 】 の解答に n＝7 を代入して、 13/27 になる。

　【 シミュレーション 】

100万回、２人の子供を作ってみます。
同様に確からしい「少なくとも１人の女の子」のある性質の分類区分数？
　 1 から 10000 までの自然数で入力してください。 個
　　　　　　＊ 生まれた曜日なら７個、 生まれた月なら 12 個
　　　　　　　 生まれた時刻が午前中か午後かならば ２個
　




プログラムの内容 ：

【 問 題 ５ 】　⇒　内蔵で理解するために

　（１）

　彼女には２人の子供がある。
　２人の子供とも、火曜日に生まれた女の子である確率はいくらか？

　　　　解答：　(1/2×1/7)²　＝→　1/196
　　　　別解：　1 / (7×2)²　＝→　1/196

　（２）

　彼女には２人の子供がある。
　２人の子供のうち、少なくとも１人が、火曜日に生まれた女の子である確率はいくらか？

　　　　解答：　1/196 ＋ 1/196 × (13＋13)　＝→　27/196

　（３）

　彼女には２人の子供がある。
　２人の子供のうち少なくとも１人は火曜日に生まれた女の子である。
　２人の子供とも、 火曜日に生まれた女の子である確率はいくらか？

　　　　解答：　1/196 ÷ 27/196　＝→　1/27
　　　　別解：　1 ÷ 27　＝→　1/27

　（４）

　彼女には２人の子供がある。
　２人の子供のうち少なくとも１人は火曜日に生まれた女の子である。
　もう一方の子供が火曜日以外に生まれた女の子である確率はいくらか？

　　　　解答：　1/196 × (6＋6) ÷ 27/196　＝→　12/27
　　　　別解：　(6＋6) ÷ 27　＝→　12/27

　（５）

　彼女には２人の子供がある。
　２人の子供のうち少なくとも１人は火曜日に生まれた女の子である。
　もう一方の子供が 火曜日に生まれた女の子であるか または 火曜日以外に生まれた女の子である 確率はいくらか？

　　　　解答：　1/27 ＋ 12/27　＝→　13/27

　　　　解説：　火曜日生まれという情報によって条件付き確率が高くなるのは、
　　　　　　　もう一方の子供が火曜日以外に生まれた女の子であっても
　　　　　　　条件満足者としてカウントされるからです。

　（６）

　彼女には２人の子供がある。
　２人の子供のうち少なくとも１人は火曜日に生まれた女の子である。
　２人の子供とも女の子である確率はいくらか？

　　　　解答： （５）と同じ問題なので、当然、同じ答え 13/27 です。

　（７）

　「 今日は沢山の２人の子供さんを持つお母様達に集まっていただき、上手な子育てについての講演を聴いていただきました。この後ですが、上のお子さんが火曜日に生まれた女の子（ 会場にいる人の 1/14 ） または 下のお子さんが火曜日に生まれた女の子（ 会場にいる人の 1/14 ） のお母達のみ会場に残ってください。これに該当されない方は退場してください。」
　「（ ５分後 ）お忙しいところ会場に足止めして申し訳ありません。皆さんの中で、上のお子さんも下のお子さんも火曜日に生まれた女の子である方（ 会場にいる人の 1/27 ）は挙手願います。」
　「 では、皆さんの中で、上のお子さんが午前中に生まれた女の子であり、下の方が午後から生まれた女の子である方（ 会場にいる人の 6/27 ）は挙手願います。」
　「 では、皆さんの中で、下のお子さんが午前中に生まれた女の子であり、上の方が午後から生まれた女の子である方（ 会場にいる人の 6/27 ）は挙手願います。」
　「 挙手されなかった方（ 会場にいる人の 14/27 ）はすべて、女のお子さんと男のお子さんとをお持ちの方ですね。」

　（８）

　「 今日は沢山の２人の子供さんを持つお母様達に集まっていただき、上手な子育てについての講演を聴いていただきました。この後ですが、上のお子さんが午前中に生まれた女の子（ 会場にいる人の 1/4 ） または 下のお子さんが午前中に生まれた女の子（ 会場にいる人の 1/4 ） のお母達のみ会場に残ってください。これに該当されない方は退場してください。」
　「（ ５分後 ）お忙しいところ会場に足止めして申し訳ありません。皆さんの中で、上のお子さんも下のお子さんも午前中に生まれた女の子である方（ 会場にいる人の 1/7 ）は挙手願います。」
　「 では、皆さんの中で、上のお子さんが午前中に生まれた女の子であり、下の方が午後から生まれた女の子である方（ 会場にいる人の 1/7 ）は挙手願います。」
　「 では、皆さんの中で、下のお子さんが午前中に生まれた女の子であり、上の方が午後から生まれた女の子である方（ 会場にいる人の 1/7 ）は挙手願います。」
　「 挙手されなかった方（ 会場にいる人の 4/7 ）はすべて、女のお子さんと男のお子さんとをお持ちの方ですね。」

　（９）

　「 今日は沢山の２人の子供さんを持つお母様達に集まっていただき、上手な子育てについての講演を聴いていただきました。この後ですが、上のお子さんが 1/15 に生まれた女の子（ 会場にいる人の 1/730 ） または 下のお子さんが 1/15 に生まれた女の子（ 会場にいる人の 1/730 ） のお母達のみ会場に残ってください。これに該当されない方は退場してください。」
　「（ ５分後 ）お忙しいところ会場に足止めして申し訳ありません。皆さんの中で、上のお子さんも下のお子さんも 1/15 に生まれた女の子である方（ 会場にいる人の 1/1459 ）は挙手願います。」
　「 では、皆さんの中で、上のお子さんが 1/15 に生まれた女の子であり、下の方が 1/15 以外に生まれた女の子である方（ 会場にいる人の 364/1459 ）は挙手願います。」
　「 では、皆さんの中で、下のお子さんが 1/15 に生まれた女の子であり、上の方が 1/15 以外に生まれた女の子である方（ 会場にいる人の 364/1459 ）は挙手願います。」
　「 挙手されなかった方（ 会場にいる人の 730/1459 ）はすべて、女のお子さんと男のお子さんとをお持ちの方ですね。」

　　参照 :　JavaScript ＞ JavaScript＿シミュレーション ＞ 不思議な条件付き確率