多人数 （ ｎ 人 ） での１発勝負ジャンケンで ｍ 人 が勝つ確率 ：

　　　すべての場合の数
　　　　　　３^ｎ とおり

　　　勝者たちが決まるのは３とおり
　　　　　　グー と チョキ だけ
　　　　　　チョキ と パー だけ
　　　　　　パー と グー だけ

　　　勝者の組み合わせ
　　　　　　_ｎＣ_ｍ とおり

　　　したがって、
　　　　　　


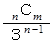
多人数 （ ｎ 人 ） での１発勝負ジャンケンで あいこ になる確率 ：
　　　　　
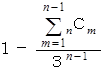
ｎ 人でじゃんけんしたときにあいこになる確率の一般的な求め方 ：

まず、 ｎ 人でじゃんけんしたときにあいこにならない確率を求める。

　　　Ａ ：　全員がグー以外を出す場合の数　＝　２ ^ｎ 通り
　　　Ｂ ：　全員がチョキ以外を出す場合の数　＝　２ ^ｎ 通り
　　　Ｃ ：　全員がパー以外を出す場合の数　＝　２ ^ｎ 通り
　　　Ｄ ：　全員がグーを出す場合の数　＝　１ 通り
　　　Ｅ ：　全員がチョキを出す場合の数　＝　１ 通り
　　　Ｆ ：　全員がパーを出す場合の数　＝　１ 通り
　　　Ｇ ：　すべての場合の数　＝　３ ^ｎ 通り

　　　｛ （ Ａ−Ｅ−Ｆ ） ＋ （ Ｂ−Ｆ−Ｄ ） ＋ （ Ｃ−Ｄ−Ｅ ） ｝ ÷　Ｇ
　　　　　　　　＝→　（ ２ ^ｎ − ２ ） × ３　÷　３ ^ｎ
　　　　　　　　＝→　（ ２ ^ｎ − ２ ） ÷　３ ^ｎ−１

最後に、 ｎ 人でじゃんけんしたときにあいこになる確率を求める。
　　　１ − （ ２ ^ｎ − ２ ） ÷　３ ^ｎ−１　＝→　（ ３ ^ｎ−１ − ２ ^ｎ ＋ ２ ） ÷　３ ^ｎ−１

あいこ になる確率をシミュレーションしてみましょう。

何人？　　　　　





　　プログラム ：