確率 へ戻る（１） スクリーニング検査 と 精密検査 との関係
-
例えばの話ですが、 国民の 11人に１人 （ ９.１％ ） があるウィルスに慢性的に感染しており、 そのウィルスに慢性的に感染している人は発癌率が若干高いため、 健康診断の項目の中にそのウィルスのスクリーニング検査 （ 簡易検査 ） が含まれているものとします。 その検査は、 感度 （ 偽陰性の少なさを表す度合い ） と 特異度 （ 偽陽性の少なさを表す度合い ） がともに90％であるとします。 Ａさんはスクリーニング検診の結果が陽性のため精密検査 （ 本当にウィルスに感染しているかどうかを調べる検査 ） が必要であるとの通知を受けました。 さて、 Ａさんがこのウィルスに感染している確率は何％でしょうか？
ヒント ： 特異度 （ 偽陽性の少なさを表す度合い ） が90％であるから、
90％であるというわけではありません。
総受診者数110人の場合で、 理論的なウィルス一次検診の結果を書き出すと、 次のような表になります。
|
|
簡易検査陽性 |
簡易検査陰性 |
合 計 |
|
ウィルス感染あり |
９人 |
１人 |
10人 |
|
ウィルス感染なし |
10人 |
90人 |
100人 |
|
合 計 |
19人 |
91人 |
110人 |
Ａさんの場合は、 スクリーニング検査陽性の19人のうちのひとりです。 この19人のうち 、ウィルスに感染している人は、 ９÷19 ≒ 47.4 % ですから、 Ａさんがこのウィルスに感染している確率は
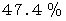です。 Ａさん、 恐がらなくていいですから、 きちんと精密検診を受けてくださいね。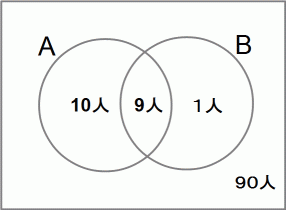
集合Ａ ： 簡易検査陽性者の集合
集合Ｂ ： ウィルス感染者の集合
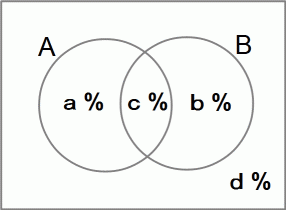
（２） 上記の問題の解説
-
確率表：
| 検査結果？ | ||||
|---|---|---|---|---|
| 陽性 | 陰性 | 計 | ||
| 有病者？ | 有病人 | 9/110 | 1/110 | 10/110 |
| 非病人 | 10/110 | 90/110 | 100/110 | |
| 計 | 19/110 | 91/110 | １ | |
① ある人が有病人の上に検査陽性である確率： 1/11 × 9/10 ＝→ 9/110
② ある人が非病人の上に検査陽性である確率： 10/11 × 1/10 ＝→ 10/110
ある人が検査陽性となる確率： ①＋② ＝→ 19/110
求める条件付き確率（ 検査陽性者が本当に有病人である確率 ）：
① ÷ ( ①＋② ) ＝→ 9/110 ÷ 19/110 ＝→ 9/19 ≒→ 47.4 %