【 問 題 １ 】

　 自然数 １ 〜 ｎ の ｎ 枚のカードが裏返しにして置かれています。 無作為に １ 枚ずつめくっていきます。 １ のカードが出てくるまでにめくるカードの数は平均何枚でしょうか？

【 解 答 】

　 ｎ 枚めくったときに １ が出てきたときに ｎ 点得るとします。 すると、 その期待値は次のようになります。
　　　　
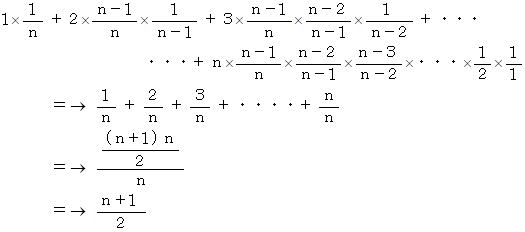
したがって、 答えは、
　　　　　　　　　　　　　



１０万回のシミュレーション ：　　ｎ ＝ 　　　



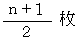
プログラム ：

【 問 題 ２ 】

　 自然数 １ 〜 ｎ の ｎ 枚のカードが裏返しにして置かれています。 無作為に １ 枚ずつめくっていきます。 自然数 １ 〜 ｍ ( ｍ ＜ ｎ ) の どれかのカードが出てくるまでにめくるカードの数の期待値は？

【 解 答 】

　　
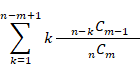
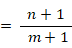
　　　　※ 参考： 式の立て方については 確率 ＞ 釣り堀の確率 を参考にしてください。
　　　　　　　　 答えの導き方は難解です。数学 超・超絶 難問（ 小野田博一 著 ）を参考にしてください。


10万回のシミュレーション ：
　　全てのくじの数 (n)：　
　　当たりくじの数 (m)：　
　　一度引いたくじは元に戻さない。
　　　



プログラム ：

【 問 題 ３ 】

　 ボタンを押すと １ 〜 ｎ の 自然数をランダムに表示してくれるマシーンがあります。 １ が表示されるまでに平均何回ボタンを押さなければならないでしょうか？

【 解 答 】

　 ｎ 回ボタンを押したときに初めて １ が表示されたときに ｎ 点得るとします。 すると、 その期待値 Ｓ は次のようになります。
　　　　
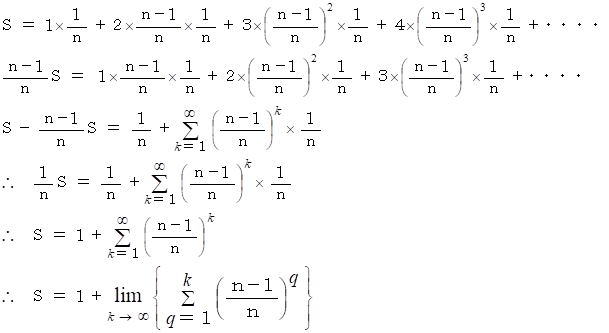
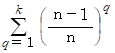は初項と公比が 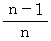の等比数列の第ｋ項までの和だから、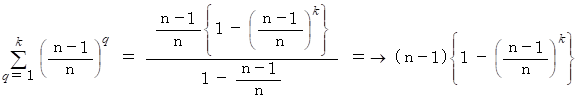
　　　　
したがって、
　　　　

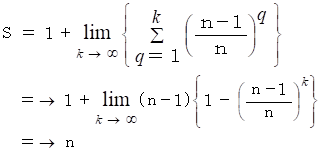
したがって、 答えは ｎ 回 です。


（ 別 解 ）
　　　　


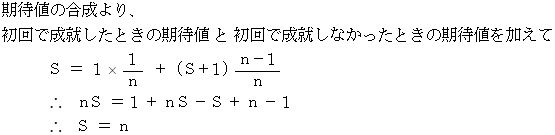
　この問題を解いて判ったことは、「１回の試行で念願成就する確率が Ｐ でずっと一定のとき、念願成就するためには平均 １/Ｐ 回 試行することが必要である。」ということです。



10万回のシミュレーション ：　　ｎ ＝ 　　　



プログラム ：

【 問 題 ４ 】

　n 個の椅子を円周上に等間隔に並べて固定します。無作為に椅子を１個選び腰掛けます。1〜n までの自然数の中から無作為に１個の数字を選び、その数だけ時計回りに椅子を移動します。このように選んだ数字のぶんだけ椅子を移動していくと平均何回で最初の椅子に戻ってくるでしょうか？

【 解 答 】

　１回の試行で念願成就する確率が 1/n でずっと一定であるので、念願成就するためには 平均 n 回 試行することが必要である。

（ 別 解 ）
　　　　



10万回のシミュレーション ：
椅子の数（ ２〜12 ）：　

　　　　

平均 回で戻った。




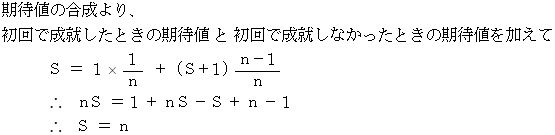
プログラム ：