解りやすくするため2次元で考えます。
直角に交わる直径を表す線分が2本描かれた半径
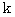 メートル の円盤があります。 円盤の表面はツルツルで摩擦が生じません。 円盤は反時計回りに角速度
メートル の円盤があります。 円盤の表面はツルツルで摩擦が生じません。 円盤は反時計回りに角速度 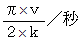 で等速回転しています。 回転している円盤上を 点O から 点A に向けて、 質量
で等速回転しています。 回転している円盤上を 点O から 点A に向けて、 質量 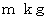 の角皿を速さ
の角皿を速さ 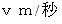 で滑らせます。 すると角皿は、 図 1 でいうと真下に向かって等速直線運動をし、 角皿が円盤の辺縁に到着する時刻
で滑らせます。 すると角皿は、 図 1 でいうと真下に向かって等速直線運動をし、 角皿が円盤の辺縁に到着する時刻 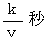 には、 点A は90度回転して円盤の右側に来ています。 角皿は滑っている間、 なにも力を受けません。
には、 点A は90度回転して円盤の右側に来ています。 角皿は滑っている間、 なにも力を受けません。*
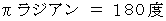
図 1
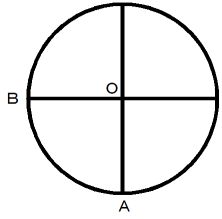
この間の角皿の円盤上の軌跡を図2に表すと、 次のようになります。
図 2
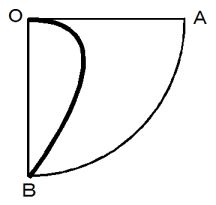
次は、 回転している円盤上を 点A から 点O に向けて、 角皿を速さ
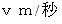 で滑らせたときの角皿の円盤上の軌跡を図3に示します。
で滑らせたときの角皿の円盤上の軌跡を図3に示します。図3
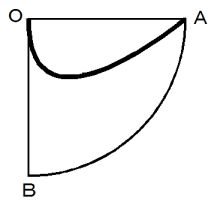
図2を、 円盤上の点A にいる観察者が見たらどうなるでしょうか?
角皿は時計回りに角速度
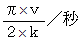 を保ったまま、 次第に回転の速さを大きくしながら円盤の外側へと移動します。 この間角皿には、 ずっと同じ大きさの力が角皿の回転の接線方向に働いています。
を保ったまま、 次第に回転の速さを大きくしながら円盤の外側へと移動します。 この間角皿には、 ずっと同じ大きさの力が角皿の回転の接線方向に働いています。図3を、 円盤上の点A にいる観察者が見たらどうなるでしょうか?
角皿は時計回りに角速度
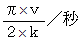 で等速回転しながら、 次第に速さを小さくしながら円盤の内側へと移動します。 この間角皿には、 ずっと同じ大きさの力が角皿の回転方向と逆向に働いています。
で等速回転しながら、 次第に速さを小さくしながら円盤の内側へと移動します。 この間角皿には、 ずっと同じ大きさの力が角皿の回転方向と逆向に働いています。このような、 円盤と一緒に回転している観察者にとっての「 みかけの力 」をコリオリの力といいます。 では、 コリオリの力の大きさを求めてみましょう。 図2で考えることにします。 線分OA や 線分OB は静止していて、 角皿が曲線運動しています。 角皿が点O を出発すると同時に、 点O を出発し線分OA に沿って速さ
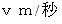 で移動する点P を考えます。
で移動する点P を考えます。
角皿が点O を出発してから
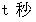 後の、 点O を中心とする 点P と 角皿の位置 とを結ぶ弧 の長さを
後の、 点O を中心とする 点P と 角皿の位置 とを結ぶ弧 の長さを 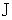 とすると、 扇形の弧長 = 中心角 × 半径 より次のようになります。( 角速度を ω とします )
とすると、 扇形の弧長 = 中心角 × 半径 より次のようになります。( 角速度を ω とします )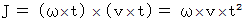
角皿の回転方向への加速度を
 とすると、 初速
とすると、 初速 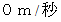 の角皿の
の角皿の  秒後の移動距離は次のようなります。
秒後の移動距離は次のようなります。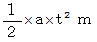
なぜなら、
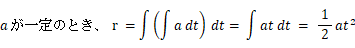
そこで、次のように置くことによって
 を求めることができます。
を求めることができます。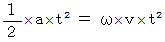
したがって、
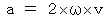 となり、 ニュートンの運動方程式を使って力が解ります。
となり、 ニュートンの運動方程式を使って力が解ります。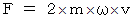
これがコリオリの力の大きさです。
コリオリの力の大きさは、 次のような方法でも求めることができます。
回転している円盤上を角皿を点O から点A に向けて速さ
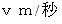 で滑らせますが、 今度は角皿に力を加え続けることによって、 結果として角皿が線分OA上を滑るようにします。 つまり、 角皿を円盤と同じ角速度の回転運動を保つようにして滑らせます。
で滑らせますが、 今度は角皿に力を加え続けることによって、 結果として角皿が線分OA上を滑るようにします。 つまり、 角皿を円盤と同じ角速度の回転運動を保つようにして滑らせます。そこで、 まず角皿の運動量モーメントを考えます。
中心からの距離(
 )、 質量(
)、 質量(  )、 速さ(
)、 速さ(  )、 時間(
)、 時間(  )、 角速度(
)、 角速度(  ) とすると、 運動量モーメント(
) とすると、 運動量モーメント(  )は、 次のように表されます。
)は、 次のように表されます。
すると、 力のモーメント(
 )は、 次のようになります。
)は、 次のようになります。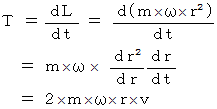
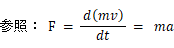
すると、 力(
 ) は、 次のようになります。 力の向きは、 円盤の回転方向で、 回転中心からの位置ベクトルに対して垂直です。
) は、 次のようになります。 力の向きは、 円盤の回転方向で、 回転中心からの位置ベクトルに対して垂直です。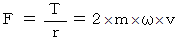
これを、 円盤上の点A にいる観察者が見ればどうでしょうか。 角皿には何も力が加わらず、 角皿は等速直線運動をしたことになります。 でも、 客観的に見ると上記の力が必要であったのです。 ということは、 力のつり合いより、 円盤と一緒に回転している観察者にとっては、 角皿には先ほどと大きさが同じで方向が正反対の力が働き続けたことになります。 これがコリオリの力です。 そうして、図2のような結果になるはずです。
 力学 へ戻る
力学 へ戻る