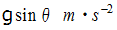転がり落ちるのは滑り落ちるのとは異なります。 傾斜角度 の摩擦ゼロの斜面を滑り落ちる物質は、 質量に関係なく、 加速度 です。 では、 質量 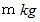、 慣性モーメント 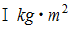、 半径 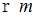の球または円柱が、 傾斜角度 の傾斜を転がり落ちるときの加速度はいくらでしょうか？

　 物質は滑り落ちようとしますので、 斜面からはそれに逆らうような摩擦力を受けます。 摩擦係数を とし、 球または円柱が受ける力を下の図に表します。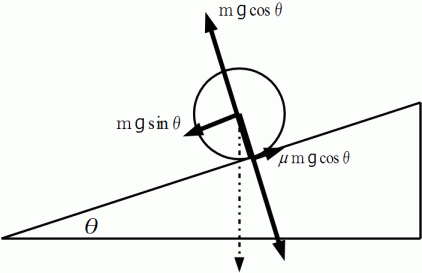

　　　　

運動方程式 ：
　　　　
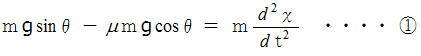
回転運動方程式 ：
　　　　

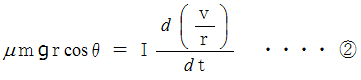
と より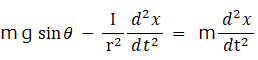
　　　　
　　　　
　　　　

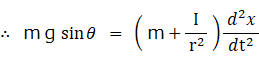
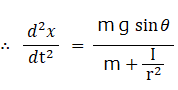
　 加速度は g sin θ より小さくなっています。 したがって、 滑り落ちるよりも転がり落ちる方が遅いことがわかります。 また、 慣性モーメントが小さいほど、 半径が大きいほど、 速く転がり落ちることもわかります。

　 私は次のパラメーターを 「 移動慣性量 」 と言っています。
　　　　　
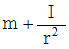
移動慣性量の単位は kg です。 移動慣性量は転がり落ちるときに加速をさせにくくする因子です。

　質量が等しくて半径が等しい次の４つのものを転がり落としたときに、早く転がり落ちる順は次のようになります。
　　　球　＞　円柱　＞　球殻　＞　円筒
なぜなら、慣性モーメントが次のようになっているからです。（　m は質量　r は半径 ）
　　　球： 2/5 m r ²　＜　円柱： 1/2 m r ²　＜　球殻： 2/3 m r ²　＜　円筒： m r ²

　　　　　　　　　　　　参考： 剛体力学 ＞ 球の慣性モーメント

※　転がり落ちる物質の中には、滑り落ちながら転がり落ちる物質が多く存在しますので、
　実験では理論値どおりにならないことがあります。