ばいおりんの慣性系相対性理論

【問題】

　小生よりも１回り若いＳ先生とＴ先生は、妻子を都会に残して単身赴任され、昼夜を問わずこの田舎の地方病院の患者さんたちの診療に当たっておられます。もちろん都会出身の先生方です。私が自宅でこの文章を書いている時間になっても、先生方はまだ病院に残っていらっしゃると思います。お二人とも小学生２人のお父さんですが、休日もほとんど家には帰っておられないようです。仕事よりも自分や家族の生活の方が大事であると考える田舎者の小生には、とうてい真似のできることではありません。

　さて、Ｓ先生の第１子は男の子であり、また、Ｔ先生にはご長男さんがいらっしゃるそうです。Ｓ先生の２番目のお子さんが女の子である確率は 50％ですが、Ｔ先生のもう一人のお子さんが女の子である確率は 50％ではありません。ではいくらなのでしょうか？

【解答】

	第２子が男の子	第２子が女の子
第１子が男の子	25％	25％
第１子が女の子	25％	25％

　今ハッキリしていることは、Ｔ先生のお子さんが２人とも女の子ではないということですから、可能性があるのは残りの３ケースです。そして、それらが起こる確率は、私がＴ先生にはご長男さんがいらっしゃるということを伺う前からすべて 25％と等しくなっていますし、私がＴ先生にはご長男さんがいらっしゃるということを伺ったからといって変化するわけでもありません。したがって、Ｔ先生のもう一人のお子さんが女の子である確率は ３分の２ ということになります。

　この問題は、確率ベン図を用いても答えを求めることができます。
　まず、集合Ａを第１子が男の子であるお父さんの集合とし、集合Ｂを第２子が男の子であるお父さんの集合として、確率ベン図を描きます。
　　　　　　　　

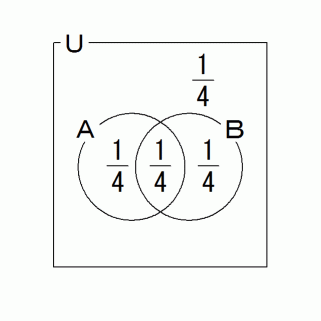
　上の図の（集合Ａまたは集合Ｂ）の補集合の部分を黒く塗りつぶして、集合Ａまたは集合Ｂを全体集合とみなします。すると、その中で（集合Ａかつ集合Ｂ）の補集合が占める割合が３分の２ということになります。