【 問 題 1 】
-
Aさんには子供が2人いる。
Aさんの子供が2人とも女の子である確率は?
-
1/4
-
Aさんには子供が2人いる。
Aさんの第1子は女の子である。
Aさんの子供が2人とも女の子である確率は?
-
1/2
Aさんの第2子が女の子である確率は 1/2 だから。
-
Aさんには子供が2人いる。早朝からずっとAさんの家の玄関前で見張っていたところ、
Aさんの子供が一人自宅から出て来たが、女の子であった。
Aさんの子供が2人とも女の子である確率は?
-
1/2 理由: 1/4 ÷ ( 1/4 + 1/4 )
| 自宅から出てこなかった子供 | ||||
|---|---|---|---|---|
| 男 | 女 | 計 | ||
| 自宅から出て来た子供 | 男 | 1/4 | 1/4 | 1/2 |
| 女 | 1/4 | 1/4 | 1/2 | |
| 計 | 1/2 | 1/2 | 1 | |
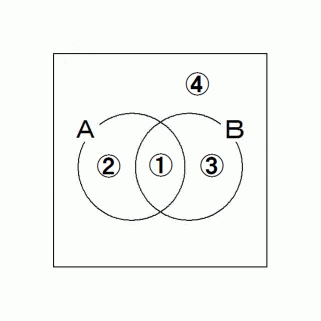
確率分布: ① + ② + ③ + ④ = 1
A: 先発命題( 真偽不明;確率的予想可 )
B: 後発命題 = 真であるという事実 = 入手情報
A
調査物質が集合Bに含まれているという情報を得た時点で、
それが集合Aにも含まれている確率が、条件付き確率 である。
条件付き確率 = ① ÷ ( ① + ③ )
B: 出てきた子であり かつ 女である子供 の集合
① 1/4 ② 1/4 ③ 1/4 ④ 1/4
求める条件付き確率: ① ÷ ( ① + ③ ) = 1/4 ÷ ( 1/4 + 1/4 ) =→ 1/4 ÷ 1/2 =→ 1/2
まず、後発命題が真である確率を求める。
-
① 先発命題が真の場合に、後発命題が真である確率:
1/2 × 1/2 =→ 1/4
③ 先発命題が偽の場合に、後発命題が真である確率:
1/2 × 1/2 =→ 1/4
次に、後発命題が真であることを知ったという条件下に、先発命題が真である確率を求める。
① を ( ①+③ ) で割る。 1/4 ÷1/2 =→ 1/2 これが条件付き確率の答えである。
-
2人とも男の子であり かつ 出て来るのが女の子である 確率: 1/4 × 0 =→ 0
男の子と女の子であり かつ 出て来るのが女の子である 確率: 1/2 × 1/2 =→ 1/4
2人とも女の子であり かつ 出て来るのが女の子である 確率: 1/4 × 1 =→ 1/4
求める確率: 1/4 ÷ ( 0 + 1/4 + 1/4 ) =→ 1/2
プログラムの内容 :
【 問 題 4 】
-
Aさんには中学生の子供が2人いる。
通りすがったときに、Aさんの子供が一人デパートの女子トイレから出て来るのを目撃した。
Aさんの子供が2人とも女の子である確率は?
-
Aさんの子どもが1人女子トイレから出て来るのを目撃されたということは、
Aさんには女の子が少なくとも1人いるということが分かったということなので。
1/3 理由: 1/4 ÷ ( 1/4 + 1/4 + 1/4 )
| 第2子 | ||||
|---|---|---|---|---|
| 男 | 女 | 計 | ||
| 第1子 | 男 | 1/4 | 1/4 | 1/2 |
| 女 | 1/4 | 1/4 | 1/2 | |
| 計 | 1/2 | 1/2 | 1 | |
-
1/2 理由: 1/2 ÷ ( 1/2 + 1/2 )
| 女子トイレから出てこなかった子供 | ||||
|---|---|---|---|---|
| 男 | 女 | 計 | ||
| 女子トイレから出て来た子供 | 男 | 0 | 0 | 0 |
| 女 | 1/2 | 1/2 | 1 | |
| 計 | 1/2 | 1/2 | 1 | |

確率分布: ① + ② + ③ + ④ = 1
A: 先発命題( 真偽不明;確率的予想可 )
B: 後発命題 = 真であるという事実 = 入手情報
A
調査物質が集合Bに含まれているという情報を得た時点で、
それが集合Aにも含まれている確率が、条件付き確率 である。
条件付き確率 = ① ÷ ( ① + ③ )
B: 出てきた子であり かつ 女である子供 の集合
① 1/2 ② 0 ③ 1/2 ④ 0
求める条件付き確率: ① ÷ ( ① + ③ ) = 1/2 ÷ ( 1/2 + 1/2 ) =→ 1/2 ÷ 1 =→ 1/2
まず、後発命題が真である確率を求める。
-
① 先発命題が真の場合に、後発命題が真である確率:
1/2 × 1 =→ 1/2
③ 先発命題が偽の場合に、後発命題が真である確率:
1/2 × 1 =→ 1/2
次に、後発命題が真であることを知ったという条件下に、先発命題が真である確率を求める。
① を ( ①+③ ) で割る。 1/2 ÷1 =→ 1/2 これが条件付き確率の答えである。
( 10万回のシミュレーション )
プログラムの内容 :
 確率 へ戻る
確率 へ戻る