【 問 題 】

赤と青の手袋と、黒と茶のマフラー。
４組の男女のペアがそれらを身に着けて、同じ家の中で待機しています。
同性どうしでは、同じコーディネート（色の組み合わせ）はありません。
まず、１組目の男女のペアが外に出てきました。

　　（１）　目撃者によると、一方の人は黒のマフラーをしているとのことです。
　　　　　　もう一方の人も黒のマフラーをしている確率はいくらですか？

　　（２）　目撃者によると、一方の人は赤い手袋に黒のマフラーをしているとのことです。
　　　　　　もう一方の人も黒のマフラーをしている確率はいくらですか？

　　（３）　目撃者によると、男性は黒のマフラーをしているとのことです。
　　　　　　女性も黒のマフラーをしている確率はいくらですか？

【 解 答 】

（１）　コーディネートを目撃された人が男性である確率は 1/2 だから、
　　　　　　　1/2 × 2/4 ＋ 1/2 × 2/4　＝→　1/2
　　　と考えるのは間違いです。ぞろ目を１通りとせず２通りとするのに似た間違いです。

　　　　コーディネートのすべての場合の数は次の４通りです。
　　　　　　　赤と黒　　　青と黒　　　赤と茶　　　青と茶

　　　　すべてのペアの場合の数は 16通り です。
　　　　そのうち、２人とも黒のマフラーのペアの場合の数は次の ４通り です。
　　　　　　　男（赤と黒） ＆ 女（赤と黒）　　　男（赤と黒） ＆ 女（青と黒）
　　　　　　　男（青と黒） ＆ 女（赤と黒）　　　男（青と黒） ＆ 女（青と黒）
　　　　そのうち、２人とも茶のマフラーのペアの場合の数は次の ４通り です。
　　　　　　　男（赤と茶） ＆ 女（赤と茶）　　　男（赤と茶） ＆ 女（青と茶）
　　　　　　　男（青と茶） ＆ 女（赤と茶）　　　男（青と茶） ＆ 女（青と茶）
　　　　どちらが黒のマフラーでもう一方が茶のマフラーのペアの場合の数は、残りの ８通り です。
　　　　「条件付き確率」の条件とは「２人とも茶色のマフラーをしているということはない」ということであり、
　　　　その条件の下で求めたいのは「２人とも黒色のマフラーをしている確率」だから、
　　　　答えは次のようになります。
　　　　　　　４ ÷ （ 16 − ４ ） ＝→　1 / 3

　　　　　　　　　　
　　　　　　　　　　
　　　　　　　　　　
　　　　　　　　　　
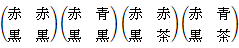
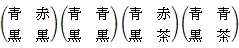
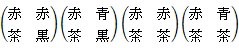
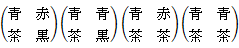
　　　　　　　第１行と第２行は、 男性が黒のマフラーをしている場合
　　　　　　　第１列と第２列は、 女性が黒のマフラーをしている場合
　　　　　　　どちらも茶のマフラーを削除すると、
　　　　　　　　　　
　　　　　　　　　　
　　　　　　　　　　
　　　　　　　　　　
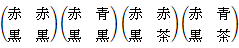
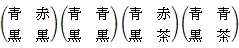
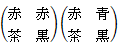
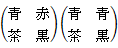
　　　　　　　　　　　　　　４ / 12　＝→　1 / 3

（２）
　　　　　　　
　　　　　　　
　　　　　　　
　　　　　　　
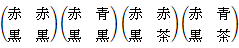
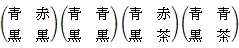
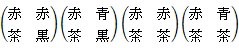
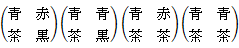
　　　　第１行は、 男性が赤い手袋に黒のマフラーをしている場合
　　　　第１列は、 女性が赤い手袋に黒のマフラーをしている場合
　　　　「条件付き確率」の条件とは、「赤と黒のコーディネートをしている人が１人以上いる」だから、
　　　　それに当てはまらないものを削除すると、
　　　　　　　
　　　　　　　
　　　　　　　
　　　　　　　

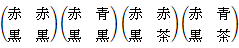
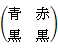
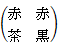
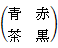
　　　　答えは、 3 / 7　です。

　　　　次のようなルールを作って、上記の図を数字に置き換えてみると、
　　　　　　　　　　　　　
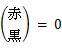
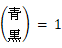
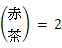
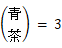
　　　　次のようになります。
　　　　　　　(0,0)　(0,1)　(0,2)　(0,3)
　　　　　　　(1,0)　(1,1)　(1,2)　(1,3)
　　　　　　　(2,0)　(2,1)　(2,2)　(2,3)
　　　　　　　(3,0)　(3,1)　(3,2)　(3,3)

　　　　どちらかが 0 であるものをピックアップすると、
　　　　　　　(0,0)　(0,1)　(0,2)　(0,3)
　　　　　　　(1,0)
　　　　　　　(2,0)
　　　　　　　(3,0)

（３）
　　　　答えは、 1 / 2　です。