確率 へ戻る（１） 条件付き確率の本質
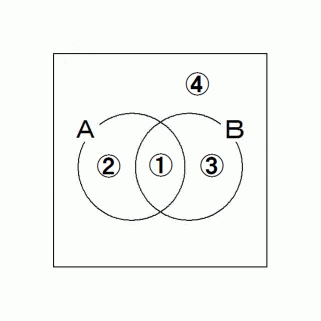
確率分布： ① ＋ ② ＋ ③ ＋ ④ ＝ １
Ａ： 先発命題（ 真偽不明；確率的予想可 ）
Ｂ： 後発命題 ＝ 真であるという事実 ＝ 入手情報
Ａ
Ｂ： 求める対象調査物質が集合Ｂに含まれているという情報を得た時点で、
それが集合Ａにも含まれている確率が、条件付き確率 である。
条件付き確率 ＝ ① ÷ ( ① ＋ ③ )
（２） 条件付き確率の解法
-
まず、その対象物が集合Ｂに属する確率を求める。つまり、後発命題が真である確率を求める。
① 対象物が集合Ａに属する確率 に 対象物が集合Ａに属する場合に集合Ｂに属する確率 をかける。
つまり、対象物が集合Ａに属する上にその対象物が集合Ｂに属する確率を求める。
③ 対象物が集合Ａに属さない確率 に 対象物が集合Ａに属さない場合に集合Ｂに属する確率 をかける。
つまり、対象物が集合Ａに属さない上にその対象物が集合Ｂに属する確率を求める。
① ＋ ③ が その対象物が集合Ｂに属する確率（ 後発命題が真である確率 ）である。
次に、その対象物が集合Ｂに属することを知ったという条件下にて、その対象物が集合Ａに属する確率を求める。つまり、後発命題が真であることを知ったという条件下にて、先発命題が真である確率を求める。
① を ( ① ＋ ③ ) で割る。これが求める 条件付き確率 である。