コイン投げの表裏 や サイコロ振りなどを数回施行したときに何回期待どおりになるのかは、 次の二項分布の公式にあてはめるだけでその確率を計算することができます。
　　　　　

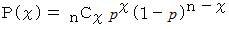
　 サイコロを６回振ったときに、 １の目の出る回数が 回 （ ＝ ０ 〜 ６ ） となる確率を求めるプログラムを十進BASIC で作ってみました。

　 このプログラムが弾き出す結果が正しいかどうかを実験で確かめるには、サイコロを６回振ったときに１の目が出た回数を帳簿に記入し、次にまたサイコロを６回振ったときに１の目が出た回数を帳簿に記入して、・・・・・と1000回繰り返して1000個のデーターを集めて、横軸に１の目が出た回数として０から６の自然数を、縦軸にその度数を1000で割った値をとって棒グラフにするといいでしょう。


　 次に、 サイコロを720回振ったときに、 １の目の出る回数が140回以上になる確率を求めるプログラムを紹介します。 これは最初に次の一行を付け加えなければ桁溢れになってうまく動きません。
　　　　　OPTION ARITHMETIC decimal_HIGH

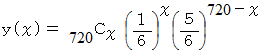　 サイコロを720回振った時に１の目の出る回数を とし、 横軸 （ ） に ０ 〜 720 の自然数をとり、 縦軸を としてグラフを描くと、 それは２項分布になります。 そして、 この二項分布は次のような正規分布に近似します。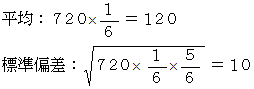
　　　　　
　 そこで、 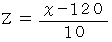と置きますと、 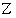は標準正規分布に従います。 そこで、 正規分布表を使って、 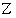が２以上になる確率を求めますと、 0.0228 となり、 プログラムで正確に求めた確率 0.0272 と若干誤差があることが解ります。