以上のことを、例を用いて確かめてみよう。

＜ 用意する３つの平面 ＞
　　　点（１，２，３）を通り、ベクトル（１，−１，−１）に直交する平面Ａ：
　　　　　　（χ−１）−（ｙ−２）−（ｚ−３）＝ ０
　　　点（２，２，１）を通り、ベクトル（１，−１，−１）に直交する平面Ｂ：
　　　　　　（χ−２）−（ｙ−２）−（ｚ−１）＝ ０
　　　点（−１，−１，１）を通り、ベクトル（２，１，４）に直交する平面Ｃ：
　　　　　　２（χ＋１）＋（ｙ＋１）＋４（ｚ−１）＝ ０

　　　＊　ベクトル（１，−１，−１）と ベクトル（２，１，４）の内積は −３ ですので、
　　　　この２つのベクトルは直交していないことが分かります。
　　　　　２つの平行な平面をそれらに直交する平面で切断した断面の直線が平行であることは
　　　　イメージしやすいので、 この例ではそれ以外の場合にしています。

平面Ａと平面Ｃの交線を求める
　　　χ−ｙ−ｚ ＝ −４　　　・・・・
　　　２χ＋ｙ＋４ｚ ＝ １　　　・・・・
　　　辺々計算： ＋より
　　　　　　χ＋ｚ ＝ −１　→→　χ ＝ −ｚ−１
　　　辺々計算： ２×−より
　　　　　　ｙ＋２ｚ ＝ ３　→→　ｙ ＝ −２ｚ＋３
　　　ｚ＝ｔ と置くと、
　　　　　　
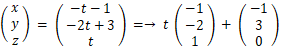
　　　したがって、平面Ａと平面Ｃの交線は、
　　　　　　　　点（−１，３，０）を通り、方向ベクトル（−１，−２，１）を持つことが分かる。

平面Ｂと平面Ｃの交線を求める
　　　χ−ｙ−ｚ ＝ −１　　　・・・・
　　　２χ＋ｙ＋４ｚ ＝ １　　　・・・・
　　　辺々計算： ＋より
　　　　　　χ＋ｚ ＝ ０　→→　χ ＝ −ｚ
　　　辺々計算： ２×−より
　　　　　　ｙ＋２ｚ ＝ １　→→　ｙ ＝ −２ｚ＋１
　　　ｚ＝ｔ と置くと、
　　　　　　
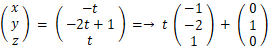
　　　したがって、平面Ｂと平面Ｃの交線は、
　　　　　　　　点（０，１，０）を通り、方向ベクトル（−１，−２，１）を持つことが分かる。

というわけで、平面Ａと平面Ｃの交線 と 平面Ｂと平面Ｃの交線 とは平行であることが分かった。