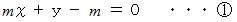
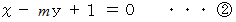
それぞれ上記の式で表される2つの直線があります。
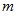 が全ての実数の範囲で変化したとき、 2つの直線の交点の軌跡は、 原点を中心とする半径 1 の円になることを証明してみましょう。
が全ての実数の範囲で変化したとき、 2つの直線の交点の軌跡は、 原点を中心とする半径 1 の円になることを証明してみましょう。 と
と  から
から 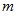 を消去して得られる x と y との関係式が、 2つの直線の交点の軌跡を示します。
を消去して得られる x と y との関係式が、 2つの直線の交点の軌跡を示します。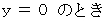
 より、
より、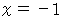
すると、
 より、
より、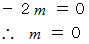
以上より、
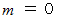 のときは、 2つの直線の交点は
のときは、 2つの直線の交点は 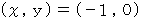
になるということである。 この交点は、 原点を中心とする半径 1 の円の上にある。
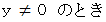
 より、
より、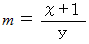
 に代入すると、
に代入すると、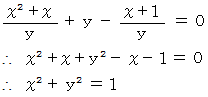
この式は、 原点を中心とする半径 1 の円を表す式である。
( 他の証明法 )
2直線の交点の公式 :
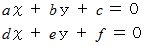
上記の2つの直線の交点は
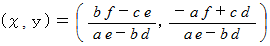
上記の公式より、 交点は次のようになる。
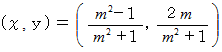
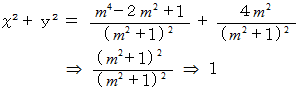
 図形の方程式 へ戻る
図形の方程式 へ戻る