半径 10 m の円周上を角速度 π/2 rad/s で反時計回りに等速円運動している観察者がいます。時刻 0 s に彼は持っていたボールをそっと手放しました。ボールの質量は 0.1 kgです。観察者の座標系におけるボールの移動について考えましょう。円の中心から観察者へ向かう方向を y 軸の向きとし、観察者の移動速度と反対方向を x 軸の向きとし、観察者は常に座標原点にいるとします。

　ボールは私たちにとっては速さ 10 × π/2 m/s　＝→　5 π m/s　で円の接線方向に等速直線運動をするのですが、観察者にとっては、最初 速さ 0 m/s で、次第に y 軸方向に加速していき、その後は次第に x 軸の正の方向へと曲がって行きます。

　観察者の座標系においてボールに作用する力は 遠心力 と コリオリの力 です。前者は、y 軸の正の方向を向いていて、大きさが　0.1 × 10 × (π/2)² N　＝→　π²/4 N　で、後者は、観察者の座標系におけるボールの速度の方向に対して垂直な方向で、かつ、x の正の方向であり、その時のボールの速さを v とすると、 2 × 0.1 × π/2 × v_ N　＝→　πv/10_N　の大きさです。

　　　　

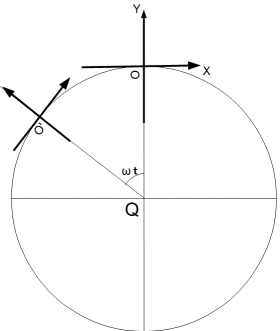
　では、もっと具合的に、観察者からはボールはどのように移動しているように見えるのでしょうか？
　ボールがリリースされた瞬間の観察者の座標系を固定したとすると、その座標系においては、ボールは x 軸の負の方向に 速さ 5 π m/s で移動していきます。でも実際は、観察者の座標系は、角速度の大きさ π/2 rad/s で反時計回りに公転しながら、角速度の大きさ π/2 rad/s で反時計回りに自転しています。そこで、まず、ボールがリリースされた瞬間の観察者の座標系を移動はさせずに自転だけさせて、その座標系でのボールの移動を考えます。すると、次のように座標変換されます。
　　　
　　　　　　
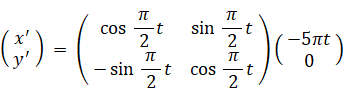
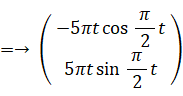
　　　　　　　　　　　参照： 力学 ＞ 等速自転座標系への座標変換

次に、これをさらに実際の観察者の座標系へと座標変換します。すると、次のようになります。
　　　
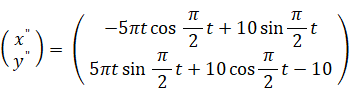
　　　　　　　　　　　参照： 大学生のための数学 ＞ その他の数学 ＞ 平行な座標系への座標変換

これが求めたいボールの運動になります。これを十進BASIC を用いてグラフにします。
ボールは１秒後には ( x, y ) ＝ ( 10, 5.71 ) の位置にあり、２秒後には ( x, y ) ＝ ( 31.42, −20 ) の位置にあります。

　　　

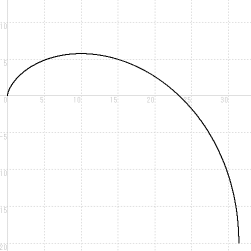
プログラムの内容 ：