(1) 正規分布に従う母集団 の 平均の区間推定 (分散が既知の場合)
-
平均が μ = ?、分散が σ2 = 16 の正規分布に従う母集団があります。そこから n = 9 個の標本を取って標本平均を求めると M = 100 でした。ここからは頭の中だけの作業ですが、その後に標本を返します。これと同じ標本平均値調査を10万回繰り返します。こうして、標本平均を確立変数とする確率分布を調べると、それは、平均が母集団の平均値(μ)に等しくて、分散が母集団の分散(σ2)を標本数(n)で割った値に等しい、正規分布 に従います。このことを「中心極限定理」といいます。( 参考: 統計学 > 中心極限定理 )
この正規分布を標準化すると次のようになります。( 参考: 統計学 > 正規分布を標準化して検定 )
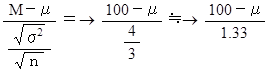
標準正規分布の 95% の臨界値 1.96 です。したがって、信頼度 95% で次の式が成り立ちます。
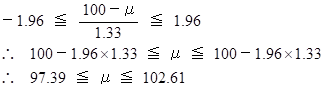
というわけで、 母集団の平均値は 95% の信頼度で 97.39 以上 102.61 以下 の範囲内にあると推定することができます。
※ 参照: 統計学 > 平均値の推定( 分散が既知の場合 )
-
正規分布に従う母集団があります。そこから標本を取って次のデーターを得ました。
標本数 9 標本平均 100 標本分散 14
9個の標本をとってその平均を求めることを1万回くり返して、次の値を確立変数とする確率分布を調べると、それは、自由度8 の t 分布に従います。
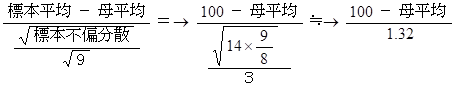
自由度8 の t 分布の95% の臨界値は 2.31 です。したがって、信頼度 95% で次の式が成り立ちます。
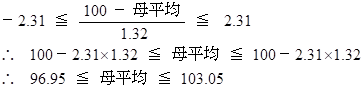
というわけで、 母集団の平均値は 95% の信頼度で 96.95 以上 103.05 以下 の範囲内にあると推定することができます。
 統計学 へ戻る
統計学 へ戻る