マクローリン展開より
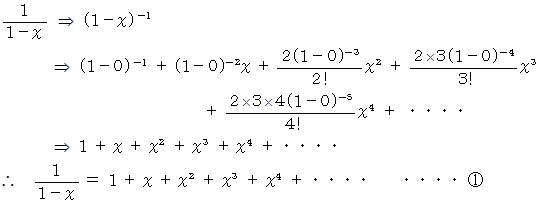
ちなみに、 マクローリン展開を用いなくても
 を導くことができます。
を導くことができます。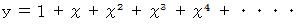
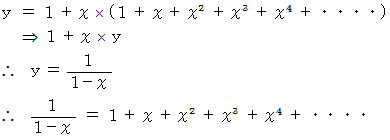
式
 の両辺を
の両辺を  で微分すると、
で微分すると、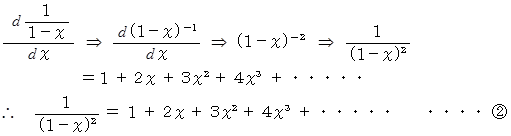
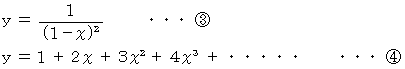
次のように、
 と
と  から
から  を導くこともできますので、
を導くこともできますので、  は間違っていません。
は間違っていません。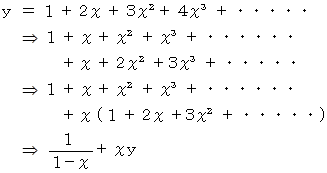
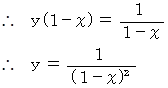
 と
と  は同じ式であるはずなのに、
は同じ式であるはずなのに、  は
は 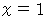 のときにのみ無限大になりますが、
のときにのみ無限大になりますが、  は
は 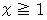 のときに無限大になります。 もし、
のときに無限大になります。 もし、  が与えられたとき、
が与えられたとき、 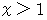 の範囲でも有限の値になるように
の範囲でも有限の値になるように  を
を  に置き換えるということをします。 これを解析接続と言います。 このように、 マクローリン展開式を 展開前の式で置き変えることもありますし、 また、 実関数を複素関数で置き変えることによって解析接続する場合もあります。 解析接続を量子物理学に応用したのが、 朝永振一郎の「 繰り込み理論 」です。
に置き換えるということをします。 これを解析接続と言います。 このように、 マクローリン展開式を 展開前の式で置き変えることもありますし、 また、 実関数を複素関数で置き変えることによって解析接続する場合もあります。 解析接続を量子物理学に応用したのが、 朝永振一郎の「 繰り込み理論 」です。 解析学 へ戻る
解析学 へ戻る