図形の方程式 へ戻る地上
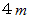の所から、 水平距離にして 
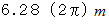先の地面に着地する方法を考えましょう。まずは、 自力で飛び降りることを考えましょう。
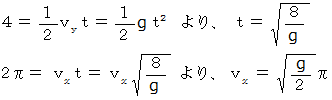
したがって、 着地地点に向かって水平方向に初速
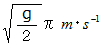で飛び出せば、 放物線を描いて目的地に着地することができます。しかし、 これは危険ですから、 安全で楽に行ける方法として、 エスカレーターを利用してみましょう。 エスカレーターでは、 乗り降りの安全を図るために、 最初と最後は地面に水平な方向に乗せた物を移動させるようなしくみになっています。 エレベーターのある階段の立ち台の面上の点、 しかもその点は次の階段との接線上にあるとします、 が描く軌道を想像しますと、 それは、 最初と最後の１割くらいが曲線で、 残りは直線になっています。 そして、 始点と終点では接線が水平方向になっています。
エスカレーターでは物足りないので、 もっとスリリングでかつ安全な方法を考えましょう。 そうです、 滑り台です。 滑り台を作るのに最も簡単なのは、
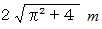の長さの板を使う方法がありますが、 それでは着地のときに危険です。 安全な着地のためには、 終点での軌道の接線が水平方向でなければなりません。 また、 スリリングにするためには、 最短時間で終点に到着するようにしてやらなければなりません。 そのためには、 始点での軌道の接線は垂直方向にすべきです。 以上の条件を満たしてくれるのが、 サイクロイド曲線 です。 このケースの軌道は次の方程式で表されます。
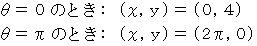
サイクロイド曲線とは、 円周上の１点が、 円が直線上を転がるときに描く軌道です。
半径 r 中心点 B の円があり、その円周上に点 A をとる。
最初、xy２次元座標の原点に点 A が来るように円を置く。
次に、円を x 軸上を正の方向に転がして、θ ラジアンだけ回転させる。
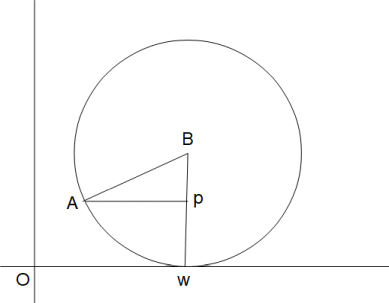
AB ＝ Bw ＝ r ∠ABw ＝ θ Ow ＝ 弧Aw ＝ r θ
A の x 座標値：
x ＝ Ow − Ap ＝→ r θ − r sinθ ＝→ r ( θ − sinθ )
A の y 座標値：
y ＝ Bw − Bp ＝→ r − r cosθ ＝→ r ( 1 − cosθ )
θ を 0 から 2π まで変化させたきに点 A が描く軌道を サイクロイド曲線 という。
最初、xy２次元座標の原点に点 A が来るように円を置く。
次に、円を x 軸上を正の方向に転がして、θ ラジアンだけ回転させる。
AB ＝ Bw ＝ r ∠ABw ＝ θ Ow ＝ 弧Aw ＝ r θ
A の x 座標値：
x ＝ Ow − Ap ＝→ r θ − r sinθ ＝→ r ( θ − sinθ )
A の y 座標値：
y ＝ Bw − Bp ＝→ r − r cosθ ＝→ r ( 1 − cosθ )
θ を 0 から 2π まで変化させたきに点 A が描く軌道を サイクロイド曲線 という。