2次元曲線:y = f (x) 上の点A( a, f (a) )における曲率半径 R を求めてみましょう。ただし、f "(a) < 0 とします。
点Aに接する円の中心を ( X, Y ) とすると、その円の方程式は次の式で表されます。
( x-X )2 + ( y-Y )2 = R2 ・・・ ①
※ ただし、f "(a) < 0 より、 a > X かつ f (a) > Y
① より、
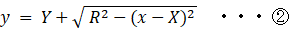
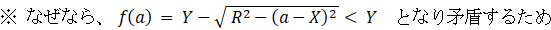
② の式を次のように置き換えます。
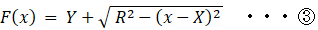
すると、次の式たちが成り立ちます。
F (a) = f (a) ・・・ ④
F '(a) = f '(a) ・・・ ⑤
F "(a) = f "(a) ・・・ ⑥
① の両辺を x で微分して、
2 ( x-X ) + 2 ( y-Y ) dy/dx = 0
よって、
( x-X ) + ( y-Y ) F '(x) = 0 ・・・ ⑦
⑦ の両辺を x で微分して、
1 + F '(x)2 + ( y-Y ) F "(x) = 0 ・・・ ⑧
⑧ の式は ( x, y ) = ( a, f (a) ) のとき成り立つので、
1 + F '(a)2 + ( f (a)-Y ) F "(a) = 0 ・・・ ⑨
⑤ と ⑥ を ⑨ に代入すると、
1 + f '(a)2 + ( f (a)-Y ) f "(a) = 0 ・・・ ⑩
よって、
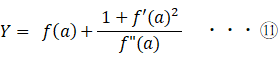
⑦ の式は ( x, y ) = ( a, f (a) ) のとき成り立つので、
( a-X ) + ( f (a)-Y ) F '(a) = 0 ・・・ ⑫
⑤ を ⑫ に代入すると、
( a-X ) + ( f (a)-Y ) f '(a) = 0 ・・・ ⑮
⑪ を ⑮ に代入して、

① の式は ( x, y ) = ( a, f (a) ) のとき成り立つので、
( a-X )2 + ( f (a)-Y )2 = R2 ・・・ ⑰
⑪ と ⑯ を ⑰ に代入して、
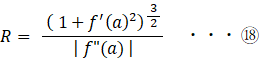
⑱ が 求めていた 2次元曲線:y = f (x) 上の点A( a, f (a) )における曲率半径です。
例えば、2次元曲線:y = sin x 上の点A( π/2, 1 )における曲率半径 ( R ) は次のようになります。
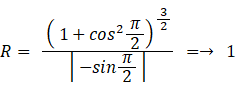
 解析学 へ戻る
解析学 へ戻る