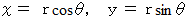 は、 直交座標系において、 極座標表示から普通の表示に変換する式たちです。
は、 直交座標系において、 極座標表示から普通の表示に変換する式たちです。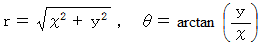 は、 普通の表示から極座標表示に変換する式たちです。
は、 普通の表示から極座標表示に変換する式たちです。普通の表示から極座標表示への変換は、 次のような構造になっています。

曲面の面積を求める二重積分については、 次の式が成り立ちます。
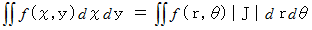
 は、 ヤコビアン といって、 ヤコビ行列の行列式のことです。 ヤコビ行列は一般的には次の行列で表されます。
は、 ヤコビアン といって、 ヤコビ行列の行列式のことです。 ヤコビ行列は一般的には次の行列で表されます。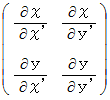
普通の表示から極座標表示に変換して曲面の面積を求める時のヤコビアンは、 次のようになります。
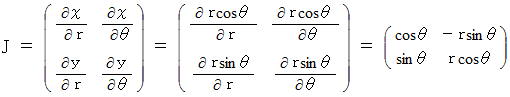
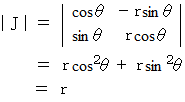
線形変換の場合は、 ヤコビ行列は座標変換テンソルの表現行列の逆行列になります。 そこで、 線形変換でない今回の場合どのようになっているのか調べてみました。 その結果は、 次のとおりです。
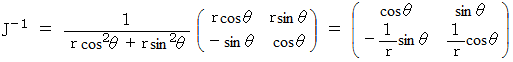
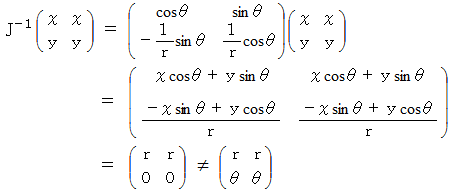
 解析学 へ戻る
解析学 へ戻る