【 問 題 】

直線　y ＝ 2 x − 2　に関する 点Ａ( 4, 1 ) の対称点( 鏡像 )を求めよ。

【 解 答 】

　　

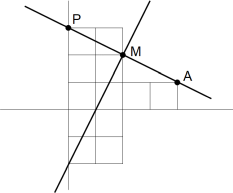
求める点を 点Ｐ( P₁, P₂ ) とする。
線分ＡＰの中点を点Ｍとすると、点Ｍの座標は次のようになる。
　　
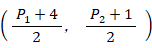
点Ａを通り、直線　y ＝ 2 x − 2　に垂直な直線の方程式は次のように表される。
　　
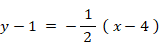
この直線を直線Ｑとする。
点Ｍは直線　y ＝ 2 x − 2　上にあるので、次の式が成り立つ。
　　　
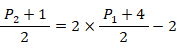
　したがって、
　　　P₂ ＝ 2 P₁ ＋ 3　　・・・ �@
点Ｍは直線Ｑ上にあるので、次の式が成り立つ。
　　
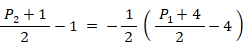
　したがって、
　　　P₁ ＝ −2 P₂ ＋ 6　　・・・ �A
�@ と �A より、 P₁ ＝ 0 ,　P₂ ＝ ３
したがって、答えは ( 0, 3 ) となる。