ベクトル解析 へ戻る曲面の表現方法 ：
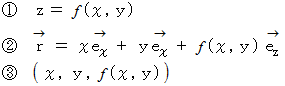
以上の３つはどれも曲面上の点を表していますが、
と 
がいろんな実数の値をとったときの点の集合が曲面になりますので、 これ自体が曲面を表しているとも言えます。 位置ベクトルを用いる 
の方法が最もアカデミックです。 位置ベクトルの起点は原点にあり終点は曲面上の点にあるように図示されることが多いようですが、 位置ベクトルの起点は曲面上の点にあると私は考えています。さて、回転しているコマの面が床と平行になっているのか、 どれくらい傾いているのかは、
から軸と床のなす角度を引けば解ります。 その結果を 
としましょう。 もし、 が 
ならばコマの面は床と平行です。 今度は、 コマの面より上に顔を出している部分の軸を、 上側を向いた大きさが 
の単位べクトルであるとします。 つまり、 コマの面にとっての単位法ベクトルですね。 すると、 そのＺ軸成分は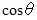 
になります。 たとえば、 Ｚ軸成分が のときは の値は です。 が ということはコマの面は床と平行であるということです。さあ、 ここからが本番です。 ＸＹ平面上の面積
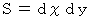の微小部分に投影される曲面の接平面の面積を 
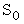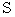とします。 接平面とＸＹ平面がなす角を とすると、 
と 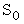の関係は次のようになります。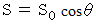
そして、
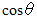は単位法ベクトルのＺ成分に等しいですので、 次のようになります。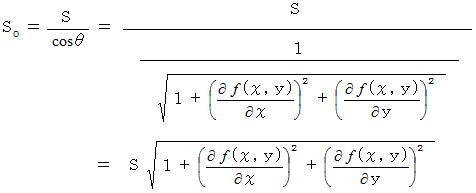
をＸＹ平面上の 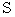の総和の部分に相当する分の総和を取れば、 その範囲でのＸＹ平面の真上にある部分の曲面の面積になりますので、 曲面の面積は次の式で表されます。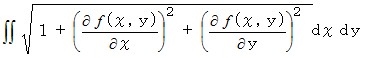
曲面上の微小部分の面積：
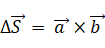
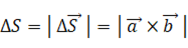
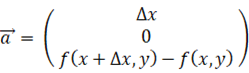
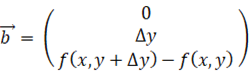
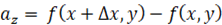
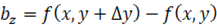
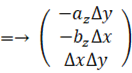
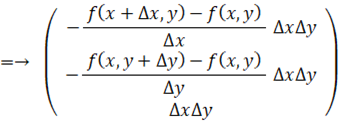
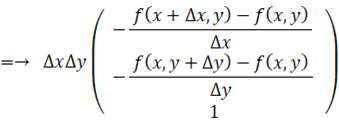
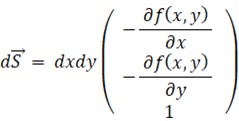
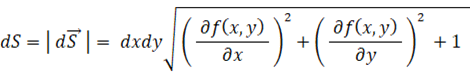____例題 ： 半径
の球の表面積を求めなさい。（ 答 え ）
中心が原点で半径
の球の方程式 ：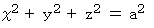 
これは次のように書くことができます。
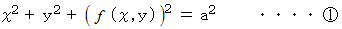
より、 ＸＹ平面よりも上にある半球の方程式は、 次のようになります。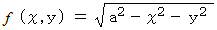
の両辺を で偏微分すると、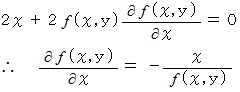
の両辺を で偏微分すると、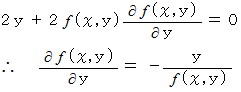
ＸＹ平面よりも上にある半球の表面積は、 次のようになります。
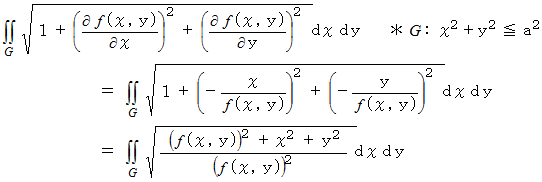
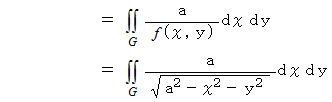
ここで、
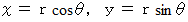と置くと、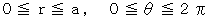
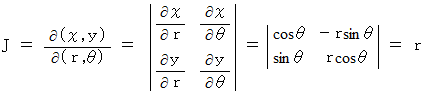
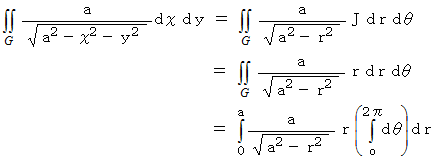
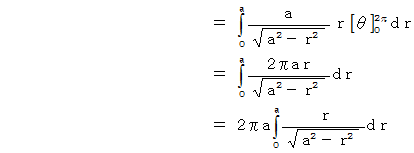
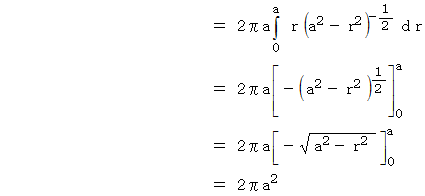
したがって、 球の表面積はその２倍の
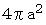になります。