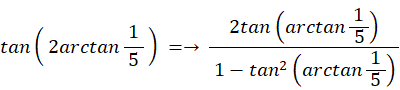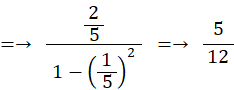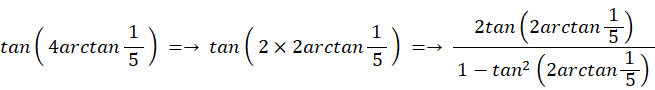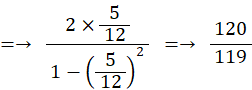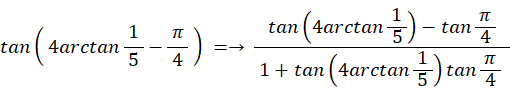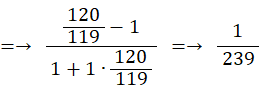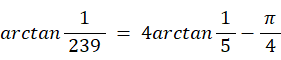ライプニッツ級数を利用して求める π の近似値:
グレゴリー級数
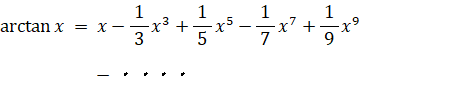
x = 1 を代入すると、ライプニッツ級数になります。
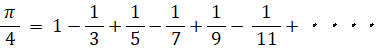
グレゴリー級数
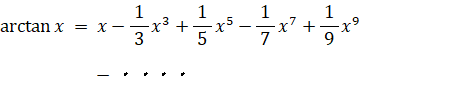
-
< グレゴリー級数の証明 >
-
マクローリン展開より
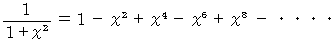
両辺を 0 〜 x まで積分すると、グレゴリー級数が得られる。
※ 参照: 解析学 > ライプニッツ級数の証明
x = 1 を代入すると、ライプニッツ級数になります。
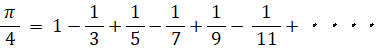
マチンの公式を利用して求める π の近似値:
次のようなマチンの公式があります。
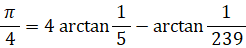
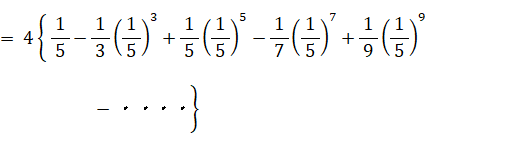
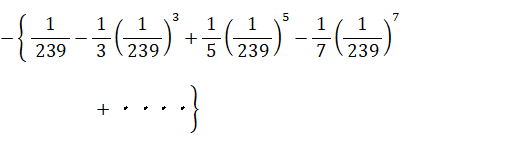
マチンの公式は収束が早いので、π の近似値を求めるのによく利用されます。
次のようなマチンの公式があります。
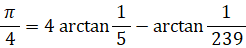
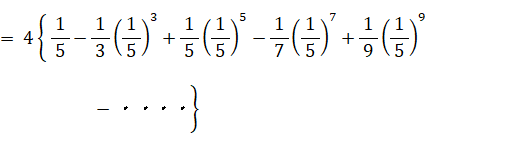
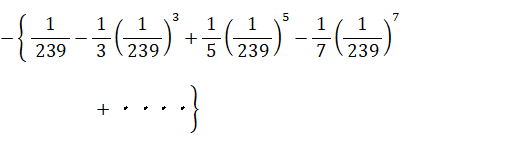
マチンの公式は収束が早いので、π の近似値を求めるのによく利用されます。
オイラー級数を利用して求める π の近似値:
π の近似値を求めるには、内接正多角形の面積を利用する方法 や オイラー級数を利用する方法 もあります。
ここでは、オイラー級数を利用する方法を紹介します。
オイラー級数:
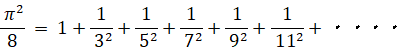
※ 参照: 数理論 > 平方数の数列の和( バーゼル問題を含む )
π の近似値を求めるには、内接正多角形の面積を利用する方法 や オイラー級数を利用する方法 もあります。
ここでは、オイラー級数を利用する方法を紹介します。
オイラー級数:
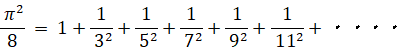
※ 参照: 数理論 > 平方数の数列の和( バーゼル問題を含む )
 解析学 へ戻る
解析学 へ戻る