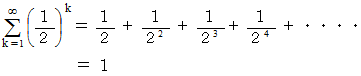
（ 証明その１ ）

　　　コインの表裏 ：　表が出れば上り
　　　　　　
　　　これらをすべて加えれば、 になる。



（ 証明その２ ）

　　　　　
　　　　　



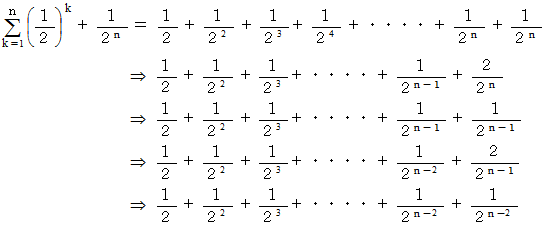
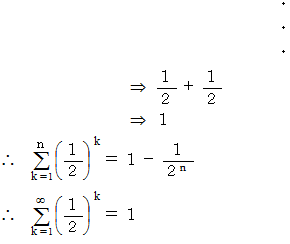
（ 証明その３ ）

　　　　　Ａ君は 100 ｍ/分 の速さで、 50 ｍ/分 の速さで逃げるＢ君を追いかけています。
　　　　今２人の距離は 100 ｍ です。　Ａ君は何分後にＢ君に追いつくでしょうか？
　　　　　　　　100 × x　＝　100 ＋ 50 × x
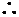　　　　　　x　＝　２

　　　　　Ａ君がＢ君が元いた所まで移動し、 それからまたＡ君がＢ君が元いた所まで移動し、
　　　　それからまたＡ君がＢ君が元いた所まで移動し、 ・ ・ ・ ・ と永遠にくり返すと、
　　　　Ａ君はＢ君に追いつくことができます。
　　　　　したがって、 Ａ君がＢ君に追いつくのに要する時間は次の式で表されます。
　　　　　　　　
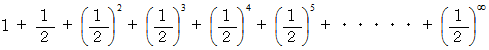
　　　　これが２分なのですから、 次の式が成り立ちます。
　　　　　　　　



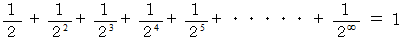
（ 証明その４ ）

　　　等比数列のｎ項までの和の公式を使うと収束値が求まります。

　　　　　



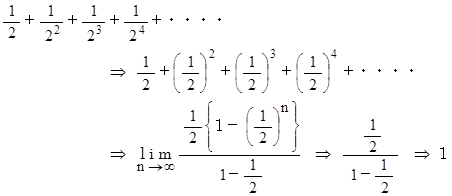
（ 証明その５ ）
　　　　　
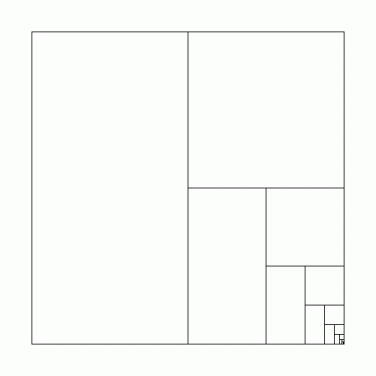
　 上の図を描く十進BASIC のプログラム ：
　　　　SET　WINDOW　-1, 11, -1, 11
　　　　PLOT　LINES : 0, 0 ; 10, 0
　　　　PLOT　LINES : 0, 0 ; 0, 10
　　　　PLOT　LINES : 10, 10 ; 10, 0
　　　　PLOT　LINES : 10, 10 ; 0, 10
　　　　LET　k = 10
　　　　LET　j = 10
　　　　FOR　i = 1　TO　20
　　　　　　IF　i/2 < > INT(i/2)　THEN
　　　　　　　　LET　k = k/2
　　　　　　　　PLOT　LINES : 10-k, 0 ; 10-k, 2*k
　　　　　　ELSE
　　　　　　　　LET　j = j/2
　　　　　　　　PLOT　LINES : 10-j, j ; 10, j
　　　　　　END　IF
　　　　NEXT　i
　　　　END