(1) 第1章
-
中心が座標原点にある半径
 の円の上半分の円周上の点における
の円の上半分の円周上の点における  座標値 と 接線の傾き との関係を求めてみましょう。
座標値 と 接線の傾き との関係を求めてみましょう。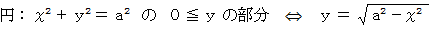 とすると、
とすると、 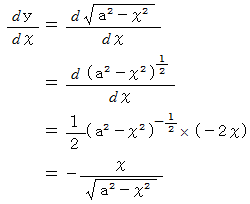
この式は、 次の章で役立ちます。
-
半径
 の球の表面上の半径
の球の表面上の半径 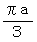 の円のエリアについて、 その面積 と 球の中心からの立体角 を考えてみましょう。
の円のエリアについて、 その面積 と 球の中心からの立体角 を考えてみましょう。半径
 の球の円周( 赤道 )の長さは
の球の円周( 赤道 )の長さは 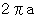 ですから、 このエリアは高さが
ですから、 このエリアは高さが 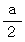 の球冠になっていることがわかります。 その球冠を真っ二つに割った時の切り口を次の図の赤色で示します。
の球冠になっていることがわかります。 その球冠を真っ二つに割った時の切り口を次の図の赤色で示します。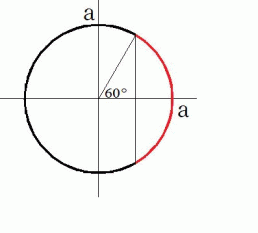
このエリア( この球冠 )の面積は次のように表されます。 なお、
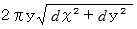 は、
は、  と
と 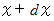 とで挟まれる部分の微小表面積を表しています。
とで挟まれる部分の微小表面積を表しています。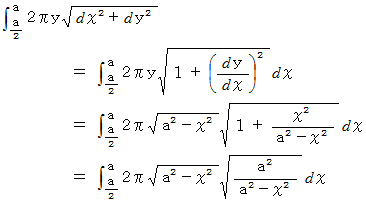
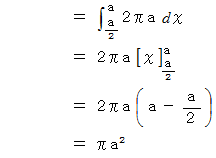
ちなみに、 半径
 の球の面積は
の球の面積は 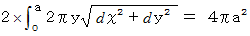 ですから、 このエリアの面積は全体の
ですから、 このエリアの面積は全体の 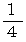 を占めています。 なお、 球の面積を導き出す式はこれ以外にもありますので、 ベクトル解析 > 曲面の面積 を参照ください。
を占めています。 なお、 球の面積を導き出す式はこれ以外にもありますので、 ベクトル解析 > 曲面の面積 を参照ください。球冠の表面上に生息するバクテリアたちからすると、半径
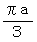 の円のエリアの面積は
の円のエリアの面積は 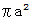 でなくて
でなくて 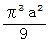 になり、
になり、 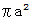 のおよそ
のおよそ 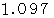 倍になります。 また、 バクテリアたちが思っているこのエリアの円周の長さは
倍になります。 また、 バクテリアたちが思っているこのエリアの円周の長さは 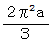 であり、 実際の
であり、 実際の 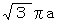 のおよそ
のおよそ 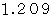 倍です。
倍です。半径
 の球の表面上の面積が
の球の表面上の面積が 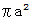 の円のエリアの 球の中心からの立体角は
の円のエリアの 球の中心からの立体角は  になります。 それは、 次の立体角の定義によります。
になります。 それは、 次の立体角の定義によります。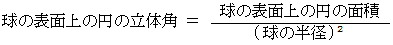
 ちなみに、 半球の立体角は
ちなみに、 半球の立体角は 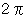 です。
です。では最後に、 半径
 の球の表面上の半径
の球の表面上の半径 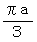 の円のエリアが作る球冠の容積はいくらになるか考えてみましょう。
の円のエリアが作る球冠の容積はいくらになるか考えてみましょう。このエリア( この球冠 )の体積は次のように表されます。 なお、
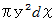 は、
は、  と
と 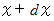 とで挟まれる部分の微小体積を表しています。
とで挟まれる部分の微小体積を表しています。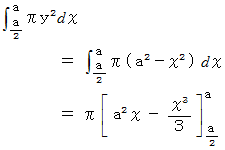
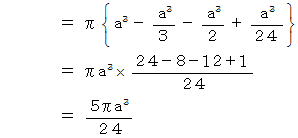
ちなみに、 半径
 の球の体積は
の球の体積は 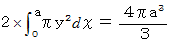 です。 球の体積を導き出す式はこれ以外にもありますので、 ベクトル解析 > 曲面の陰が作る立体の体積 を参照ください。
です。 球の体積を導き出す式はこれ以外にもありますので、 ベクトル解析 > 曲面の陰が作る立体の体積 を参照ください。 解析学 へ戻る
解析学 へ戻る