【 問 題 １ 】

　半径 ｒ の半球の体積 と 底面の半径と高さが共に ｒ の円錐の体積の和は、底面の半径と高さが共に ｒ の円柱に等しいことを示せ。

　【 解 答 】

　半径 ｒ の半球の体積は、 半球の底面から x 離れた断面（ 円 ） の面積を　０ ＜ x ＜ ｒ　の範囲で積分したものになる。
半径 ｒ の半球の底面から x 離れた断面（ 円 ） の半径は 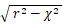である。
したがって、半径 ｒ の半球の体積は次のようになる。
　　　　

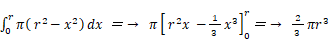
　底面の半径と高さが共に ｒ の円錐の体積は、円錐の底面から χ 離れた断面（ 円 ） の面積を　０ ＜ x ＜ ｒ　の範囲で積分したものになる。
半径 ｒ の半球の底面から x 離れた断面（ 円 ） の半径は 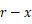である。
したがって、底面の半径と高さが共に ｒ の円錐の体積は次のようになる。
　　　　

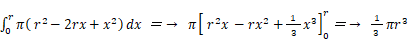
　底面の半径と高さが共に ｒ の円柱の体積は、円柱の底面から x 離れた断面（ 円 ） の面積を　０ ＜ x ＜ ｒ　の範囲で積分したものになる。
半径 ｒ の半球の底面から x 離れた断面（ 円 ） の半径は 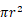である。
したがって、 底面の半径と高さが共に ｒ の円柱の体積は次のようになる。
　　　　

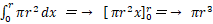
さて、次の式が成り立つ。
　　　　
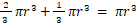
　したがって、 半径 ｒ の半球の体積 と 底面の半径と高さが共に ｒ の円錐の体積の和は、底面の半径と高さが共に ｒ の円柱に等しい。

【 問 題 ２ 】

半径 ｒ の球の表面積は、半径 ｒ の球の体積を ｒ で微分したものに等しいことを示せ。

　【 解 答 】

極座標表示で考える。
半径 ｒ の半球の中心から r sin θ 離れた断面 （ 円 ） の半径は r cos θ である。
　半径 ｒ の球の表面積の半分は、 半径 ｒ の半球の中心から r sin θ 離れた断面 （ 円 ） の円周の長さを　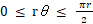　の範囲で積分したものになる。 ( r θ は弧長を表す )
したがって、 半径 ｒ の球の表面積は次のようになる。
　　　　

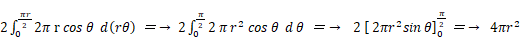
さて、半径 ｒ の球の体積は 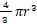である。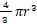
を r で微分すると 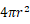になる。
　したがって、 半径 ｒ の球の表面積は、 半径 ｒ の球の体積を ｒ で微分したものに等しい。