（１） 球帯と球冠の面積

中心 （ ０，０ ）， 半径 の円の方程式 ：　　　

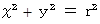
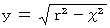
　　球帯の面積 ：
　　　　　
　　　　　

　　　　　　　　　　　　　　


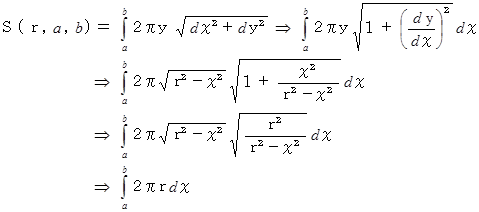
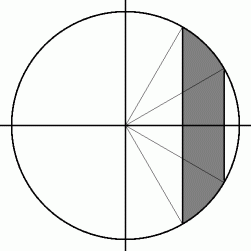
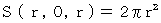　 　は、 半径 の球の表面積の半分を表します。
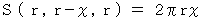　 　は、 球の表面上の点から球の中心に向かって x の距離の所で切り取ってできる球冠の面積を表し、 それが x に比例していることを表しています。 ということは、 同じ球からできる球冠や球帯は切り取る幅の長さが同じであればどこで切ってもその表面積が等しいことを示しています。
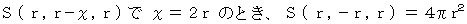　 　は、 球の表面積を表します。
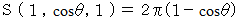　 は、 半径１の球を中心から 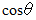の距離のところで切断して得られる球冠の表面積を表します。

（２） 立体角

　 立体角は２次元における角を３次元に拡張したもので、 円錐の頂点の立体角の大きさは、 半径 の球の中心にその円錐を頂点を重ねた時にその円錐によって切り取られる球面の面積とします。
　 偏角 ２ の円錐 （ 頂角 ２ の二等辺三角形を底辺の垂直二等分線を軸に回転してできる円錐 ） の頂点の立体角は 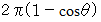です。 したがって、 半円球の立体角は ２ です。

（３） 地球儀の確率

　 地球儀の表面から無作為に１点を選んだとき、 それが北緯30度から60度の範囲に入っている確率について考えてみましょう。 それは、 その範囲の面積の地球儀の表面積に対する比率と同じす。 したがって、 次のようになります。

　　　

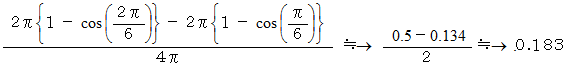
　※ 参照： JavaScript ＞ JavaScript＿シミュレーション ＞ 地球儀の１点を選んだときの緯度の確率