フーリエ変換 と ラプラス変換（ AI の回答 ）：

　フーリエ変換 と ラプラス変換 は、どちらも波や信号を数学的に扱うための手法ですが、フーリエ変換は主に 定常的な波の周波数成分を分析する のに適しており、ラプラス変換は 時間とともに変化・減衰する信号 や 複雑な微分方程式の解法 に用いられます。
　フーリエ変換は、時間とともに変化する複雑な信号を、異なる周波数を持つ単純なサイン波やコサイン波の組み合わせに分解する数学的な手法です。これにより、信号の周波数成分やその強度を分析することが可能になります。
　ラプラス変換は、時間領域の関数を s 領域の関数に変換する数学的な手法です。これにより、微分方程式の計算が代数的な演算に置き換えられ、複雑な微分方程式を容易に解くことが可能になります。

　　フーリエ変換：
　　　　
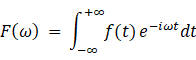
　　ラプラス変換：
　　　　
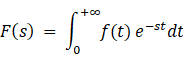
　　　　　　　　　※　s は複素数

　フーリエ変換では、指数が時間によって変化する虚数になっている e をかけてから積分しますが、ラプラス変換では、指数が時間によって変化する虚数になっている e と 指数が負の実数になっている e とを かけてから積分します。その意味は、時間がたつと減衰して収束するようにするためです。

　ラプラス変換を行って t 領域で計算するところを s 領域で簡単に計算してから、逆ラプラス変換を行って t 領域に戻してやります。言い方が正確ではありませんがイメージとしては、s 領域では、微分は掛け算に積分は割り算になります。
　ラプラス変換や逆ラプラス変換を行うには、ラプラス変換表を用いると便利です。ラプラス変換表は、例えば金沢工業大学の KIT数学ナビゲーション などにあります。
　　https://w3e.kanazawa-it.ac.jp/math/category/bibun/Laplace-henkan/henkan-tex.cgi?target=/math/category/bibun/Laplace-henkan/laplace_henkan_taiouhyou.html