特殊相対性理論を学んでいる人は、「物質の移動を表す時空間の位置ベクトルの大きさは、ローレンツ変換によって変化する。」ことをよく知っていると思うのですが、どうもそれは勘違いのようで、ローレンツ変換は、時空間の位置ベクトルの表現方法の変換であって、位置ベクトルそのものは変化せず、したがってその大きさも変化させません。その謎を解くキーワードは「斜交座標系での位置ベクトルの大きさの求め方」にあります。今回は、その謎に迫りましょう。

　　　
　　　
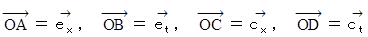
　　　点Ｐの位置ベクトル：
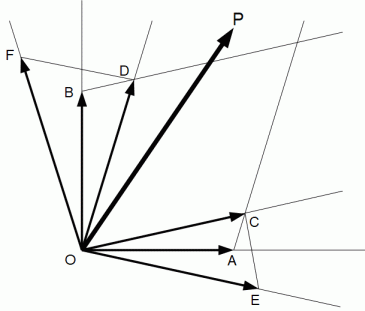
　　　　　　直交座標系：　
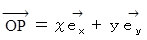
　　　　　　斜交座標系：　

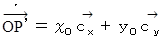
直交座標系の基底：　
斜交座標系の基底：　

ローレンツ変換の基底変換：
　　　
　　　この式は、次の式と同じです。
　　　　　　
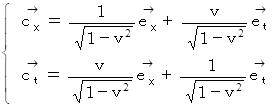
　　　ちなみに、
　　　　　　
　　　　　　
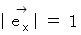
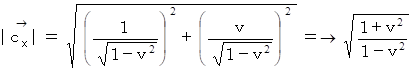
　　　　　　ローレンツ変換により、基底の要素は大きさは 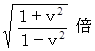になります。

ローレンツ変換の座標変換：
　　　
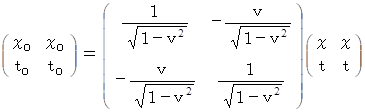
　　　この式は、次の式と同じです。
　　　　　　
　　　ちなみに、
　　　　　　

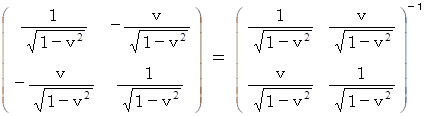
斜交座標系の基底 が作るベクトル空間の計量テンソル：
　　　

　　　
　　　

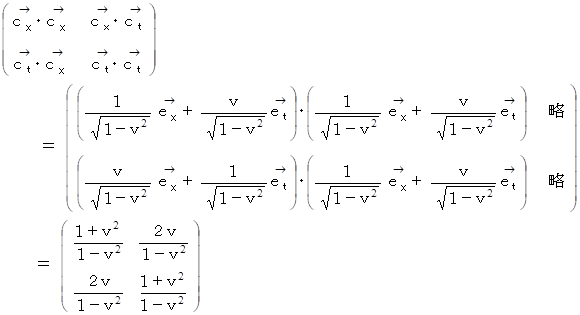
斜交座標系の基底 の双対ベクトル空間の基底：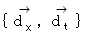　

共変基底から反変基底への座標変換：
　　　
　　　ちなみに、
　　　　　　

反変ベクトルから共変ベクトルへの座標変換：
　　　
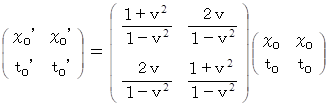
　　　この式は、次の式と同じです。
　　　　　　

点Ｐの位置ベクトルの大きさ：
　　　
　　　

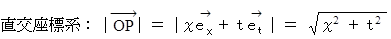
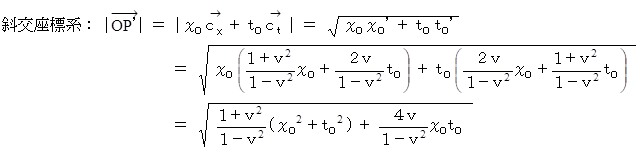
いよいよ結論です。
　　　
　　　
　　　
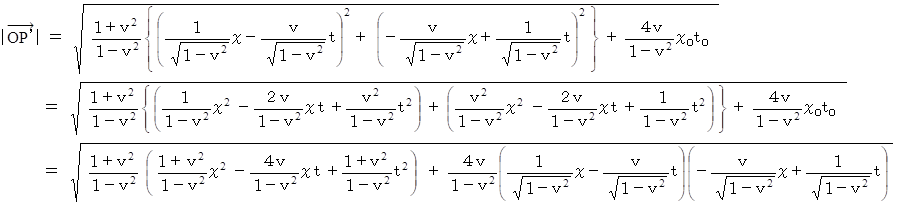
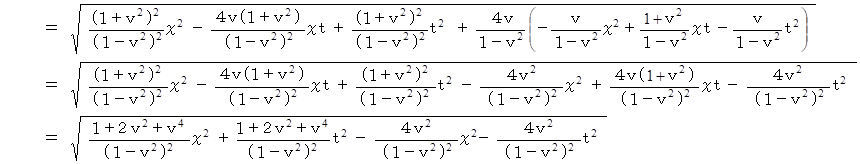
したがって、ローレンツ変換ではベクトルの大きさは変化しないことが分かりました。
じゃあ、ローレンツ変換で時間や空間の長さが変化するってどういうこと？
　　　⇒　ばいおりんのその他の相対論関連論文集 ＞ 写像 と 座標変換（ 直交 → 斜交 ）の違い